Cho hàm số f(x) xác định với x khác 0;1 và f(x) + f(1/(1-x))=x .
Tìm f(x)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Có bao nhiêu giá trị m nguyên để hàm số f(x) = 2 x 2 + m x + 2 3 2 xác định với mọi x ∈ ℝ ?
A. 5
B. 4
C. 7
D. 9
Chọn C
Hàm số f(x) =
2
x
2
+
m
x
+
2
3
2
xác định với mọi
x
∈
ℝ
![]()
![]()
Vì m nguyên nên ![]()
Vậy có tất cả 7 giá trị m thỏa mãn điều kiện đề bài.
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
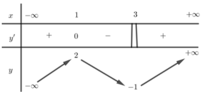
Số nghiệm của phương trình f(x) + 1 = 0 là:
A. 3.
B. 0.
C. 1.
D. 2.
![]()
Quan sát bảng biến thiên ta thấy phương trình này có 2 nghiệm.
Chọn D
cho f(x) là hàm số xác định với mọi x thỏa mãn điều kiện f(x1.x2)=f(x1).(x2)và f(2)=10 tính f(32)
cho hàm số y =ax [a khác 0] đi qua điểm A[2;1]
1/ Xác định giá trị của a.
2/ Vẽ đồ thị hàm số trên với a vừa xác định.
Cho f(x) là hàm số xác định với mọi x thỏa mãn điều kiện f(x1.x2)=f(x1).f(x2) và f(2)=10.Tính f(32)
cho hàm số f(x) xác định với mọi x và thỏa mãn f(x)+2f(1/x)=x^2. Tính f(1/3)
$f(x)$ không xác định tại $x=0$
Lời giải:
Với điều kiện đã cho thì hàm số không xác định tại $x=0$ bạn nhé
Ta có:
$f(x)+2f\left(\frac{1}{x}\right)=x^2(1)$
Cho $x\to \frac{1}{x}$ thì $f\left(\frac{1}{x}\right)+2f(x)=\frac{1}{x^2}$
$\Rightarrow 2f\left(\frac{1}{x}\right)+4f(x)=\frac{2}{x^2}(2)$
Lấy $(2)-(1)$ thì 3f(x)=\frac{2}{x^2}-x^2$
$\Rightarrow f(x)=\frac{2}{3x^2}-\frac{x^2}{3}$
$\Rightarrow f\left(\frac{1}{3}\right)=\frac{161}{27}$
Cho hàm số f(x) xác định trên ℝ \ − 1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ. Hỏi mệnh đề nào dưới đây sai?
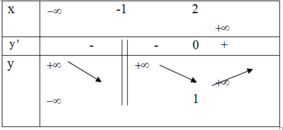
A. Đồ thị hàm số có tiệm cận đứng là x =-1
B. Hàm số đạt cực trị tại điểm x = 2.
C. Hàm số không có đạo hàm tại điểm x =-1.
D.Đồ thị hàm số có tiệm cận ngang là y =-1.
Đáp án D
Dựa vào bảng biến thiên, ta có lim x → 1 y = ± ∞ ⇒ x = − 1 là TCĐ của đồ thị hàm số
Và lim x → ± ∞ y = + ∞ suy ra hàm số không có tiệm cận ngang
Cho hàm số y=ax ( a khác 0 ) đi qua điểm A ( 2;1)
a) Xác định giá trị của a .
b) Biết M (-6;a) , E(b;3) thuộc đồ thị hàm số . Tìm a,b
Cho hàm số y=ax ( a khác 0 ) đi qua điểm A ( 2;1)
a) Xác định giá trị của a .
b) Biết M (-6;a) , E(b;3) thuộc đồ thị hàm số . Tìm a,b
bcbabcbnabchhh44GVG4vbyu72!@#$#%$%^&*())_))((*&$#@!@$^&*((I*&%#!@@#$%^&&**()*(&E#@!@#$%^&*()________)(*&^%$#@!@#$%^&*()(*&^%$#@!@#$%^&*()_)(*&^%$#@#$%^&*()_+_)(*&^%$#$%^&*()_+)(*&^%$^&*&^%$^&*^%&^%&^%$%^&*^%$#$%^&*(*&^%$##$%^&*()))))))))))))))))))))))))))))))))))))))))))))()*&^%$$$$$$$$#!#$%^&*(
cái gì vậy cha nội
a) Vì A(2;1) thuộc đồ thị hàm số y=ax
=> 1 = a.2 => a = \(\frac{1}{2}\)
b) Vì M(-6;a) thuộc đồ thị hàm số \(y=\frac{1}{2}x\)
\(\Rightarrow a=\frac{1}{2}\cdot-6=-3\)
Vì E(b;3) thuộc đồ thị hàm số \(y=\frac{1}{2}x\)
\(\Rightarrow3=\frac{1}{2}\cdot b\Rightarrow b=3:\frac{1}{2}\)
\(\Rightarrow b=3\cdot2=6\)