Gọi \(M\left(x_o;y_o\right)\) là điểm cố định mà đường thẳng \(\left(dm\right):y=mx-2m+1\) luôn đi qua 

\(\Leftrightarrow y_o=mx_o+2m+1\)

\(\Leftrightarrow m\left(x_o+2\right)+1-y_o=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_o+2=0\\1-y_o=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_o=-2\\y_o=1\end{matrix}\right.\)

\(\Leftrightarrow M\left(-2;1\right)\) là điểm cố định mà đường thẳng \(\left(dm\right)\) luôn đi qua \(\left(đpcm\right)\)

a/ Gọi điểm cố định \(M\left(x_0;y_0\right)\)

Khi đó đường thẳng y = k(x+3)-7 đi qua M , tức \(k\left(x_0+3\right)-7-y_0=0\) 

Vì đường thẳng y = k(x+3)-7 luôn đi qua M nên \(\hept{\begin{cases}x_0+3=0\\-y_0-7=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-3\\y_0=-7\end{cases}}\)

Vậy đường thẳng đã cho luôn đi qua điểm M(-3;-7)

b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)

Vì họ đường thẳng (m+2)x + (m-3)y -m+8 = 0 luôn đi qua N nên : 

\(\left(m+2\right).x_0+\left(m-3\right).y_0-m+8=0\)

\(\Leftrightarrow m\left(x_0+y_0-1\right)+\left(2x_0-3y_0+8\right)=0\)

Ta có \(\hept{\begin{cases}x_0+y_0-1=0\\2x_0-3y_0+8=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=2\end{cases}}\)

Vậy điểm cố định N(-1;2)

Câu còn lại bạn làm tương tự nhé ^^

c/ Đơn giản thôi mà =)

Ta cũng gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)

Vì họ đường thẳng y=(2-k)x+k-5 đi qua M nên : 

\(y_0=\left(2-k\right)x_0+k-5\Leftrightarrow k\left(1-x_0\right)+\left(2x_0-y_0-5\right)=0\)

Ta có \(\hept{\begin{cases}1-x_0=0\\2x_0-y_0-5=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=1\\y_0=-3\end{cases}}\)

Vậy điểm cố định là M(1;-3)

Gọi 2 điểm cố định là \(A\left(x_0;y_0\right)\)

Thay vào ptđt (d) ta được : \(y_0=mx_0+m+1\Leftrightarrow mx_0+m+1-y_0=0\)

\(\Leftrightarrow m\left(x_0+1\right)+\left(1-y_0\right)=0\)

Đẳng thức xảy ra khi \(\hept{\begin{cases}x_0+1=0\\1-y_0=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\Rightarrow A\left(-1;1\right)\)

Vậy d luôn đi qua 1 điểm cố định A(-1;1) 

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình :

14.x2=x−114.x2=x−1

<=> x² = 4x - 4

<=> x² - 4x + 4 = 0 <=> (x - 2)² = 0 <=> x - 2= 0 <=> x = 2

=> y = 2-1 = 1

Vậy (P) cắt (d) tại 1 điểm duy nhất là (2;1) 

=> đpcm 

đúng ko ????????????? 

sai thì cho mik xin lỗi

Chứng minh họ đường thẳng y = mx + (2m + 1) (1) luôn đi qua một điểm cố định nào đó.

Giả sử điểm A( x o ;  y o ) là điểm mà họ đường thẳng (1) đi qua với mọi m. Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).

Với mọi m, ta có:  y o  = m x o  + (2m + 1) ⇔ ( x o  + 2)m + (1 – y) = 0

Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.

Suy ra:  x o  + 2 = 0 ⇔  x o  = -2

1 –  y o  = 0 ⇔  y o = 1

Vậy A(-2; 1) là điểm cố định mà họ đường thẳng y = mx + (2m + 1) luôn đi qua với mọi giá trị m.

Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà \(\left(d\right)\) luôn đi qua

\(\Leftrightarrow y_0=\left(1+m\right)x_0-2m+4=x_0+mx_0-2m+4\\ \Leftrightarrow m\left(x_0-2\right)+\left(x_0-y_0+4\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=2\\2-y_0+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=6\end{matrix}\right.\)

Vậy \(\left(d\right)\) luôn đi qua \(A\left(2;6\right)\) cố định với mọi m

y=m(x-2)+1

=>m(x-2)-y+1=0

Điểm mà (d) luôn đi qua có tọa độ là:

x-2=0 và 1-y=0

=>x=2 và y=1

c) Giả sử đường thẳng  d 1  luôn đi qua một điểm cố định ( x 1 ; y 1  ) với mọi giá trị của m.

⇒  y 1 = m x 1  + 2m - 1 với mọi m

⇔ m( x 1  + 2) - 1 -  y 1 = 0 với mọi m

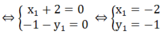
Vậy điểm cố định mà d 1  luôn đi qua với mọi giá trị của m là (-2; -1).

Giả sử ( x 0 ; y 0  ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.

Ta có:

m x 0  + 3 + (3m - 1)  y 0  = 0 với mọi m

⇔ m x 0  + 3 + 3m y 0  - y 0  = 0 với mọi m

⇔ m( x 0  + 3 y 0 ) + 3 - y 0 = 0 với mọi m

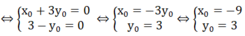
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)