trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0

Những câu hỏi liên quan
trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
−
2
x
−
4
y
+
2
0
. Phép đối xứng qua tâm O biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau: A.
(
x
−
1
)
2
+
(...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn (C): x 2 + y 2 − 2 x − 4 y + 2 = 0 . Phép đối xứng qua tâm O biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau:
A. ( x − 1 ) 2 + ( y − 2 ) 2 = 3
B. ( x + 2 ) 2 + ( y + 1 ) 2 = 3
C. ( x + 1 ) 2 + ( y + 2 ) 2 = 3
D. ( x + 1 ) 2 + ( y − 2 ) 2 = 3
Đáp án C
(C) có tâm I(1;2) bán kính R = 3
Đ O : I → I’(–1;–2)
Phương trình đường tròn (C’): x + 1 2 + y + 2 2 = 3
Đúng 0
Bình luận (0)
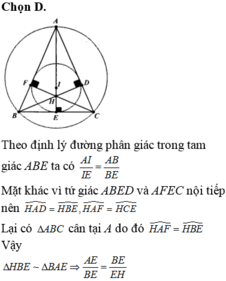
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC cân tại A(0;7) tâm đường tròn nội tiếp là điểm I(01). Gọi E là trung điểm của BC, H là trực tâm tam giác ABC. Biết AH7HE và B có hoành độ âm. Tính xB+2xC A.1 B.
3
2
C.2 D.
2
2
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC cân tại A(0;7) tâm đường tròn nội tiếp là điểm I(01). Gọi E là trung điểm của BC, H là trực tâm tam giác ABC. Biết AH=7HE và B có hoành độ âm. Tính xB+2xC
A.1
B. 3 2
C.2
D. 2 2
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (Oxy) cắt mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3
2
16
th...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (Oxy) cắt mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 16 theo giao tuyến là đường tròn tâm H, bán kính r. Tìm tọa độ tâm H và bán kính r.
A. H 1 ; 2 ; 0 , r = 7
B. H 0 ; 0 ; 3 , r = 7
C. H 1 ; 2 ; 0 , r = 7
D. H 1 ; 2 ; 0 , r = 11
Trong mặt phẳng hệ trục tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I; E (1/2;1/2) là trung điểm AB. H (4/5;-22/5) là tọa độ hình chiếu vuông góc của A lên CI. Ptdt BC : x+y-4=0. Tìm tọa độ A,B,C
Trong hệ trục Oxy cho ba điểm A(1;1) ; B(4;1) ; C(1;5) . Xác định tọa độ tâm đường tròn nội tiếp ∆ABC
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) α. Giả sử điểm M có tọa độ (xo; yo).Hãy chứng tỏ rằng sinα yo, cosα xo, tanα yo/xo , cotα xo/yo .
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) = α. Giả sử điểm M có tọa độ (xo; yo).
Hãy chứng tỏ rằng sinα = yo, cosα = xo, tanα = yo/xo , cotα = xo/yo .
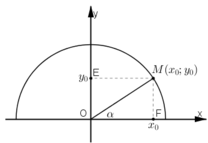
Gọi E, F lần lượt là hình chiếu của M trên Oy, Ox.
Khi đó xét ΔMOF vuông tại F thì :
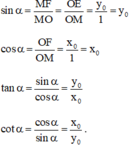
Đúng 0
Bình luận (0)
Trong hệ trục tọa độ Oxy, cho điểm I(1;1) và đường thẳng (d):3x+4x-20 Đường tròn tâm I và tiếp xúc với đường thẳng (d) có phương trình A.
x
-
1
2
+
y
-
1
2...
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho điểm I(1;1) và đường thẳng (d):3x+4x-2=0 Đường tròn tâm I và tiếp xúc với đường thẳng (d) có phương trình
A. x - 1 2 + y - 1 2 = 5 .
B. x - 1 2 + y - 1 2 = 25 .
C. x - 1 2 + y - 1 2 = 1 .
D. x - 1 2 + y - 1 2 = 1 5 .
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác nhọn ABC có B(-1,-2) và C(6,-1) nội tiếp đường tròn tâm I(2,2) .Gọi M là trung điểm AC , H là hình chiếu vuông góc của M lên AB .Tìm tọa độ của A biết rằng H thuộc đường thẳng 5x-y-1 =0 và hoành độ dương .