Trong không gian Oxyz, cho 2 điểm A(2;-1;2), B(0;1;0) bán kính R=3 là
A. x 2 + y 2 + z 2 + 4 x - 2 y - 6 z + 5 = 0
B. x 2 + y 2 + z 2 + 4 x - 2 y + 6 z - 5 = 0
C. x 2 + y 2 + z 2 + 4 x - 2 z + 5 = 0
D. x 2 + y 2 + z 2 + 4 x + 2 y + 6 z - 5 = 0
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB 2/3. Khi đó độ dài OM lớn nhất bằng: A. 6
3
B. 12
3
C.
5
3
2
D. 5
3
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:
A. 6 3
B. 12 3
C. 5 3 2
D. 5 3
Chọn B
Gọi M (x; y; z)
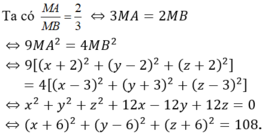
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(-1; 2; 3). Tính khoảng cách giữa hai điểm AB
A. A B = 17
B. A B = 13
C. A B = 14
D. A B = 19
Trong không gian Oxyz, cho hai điểm A(1;-1;2) và B(2;1;1). Tính
A
B
→
2
A. 2 B. 6 C.
2
D.
6
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;-1;2) và B(2;1;1). Tính A B → 2
A. 2
B. 6
C. 2
D. 6
cho mình hỏi vs
câu 1 trong không gian hệ trục tọa độ Oxyz cho mặt phẳng (A) đi qua hai điểm A( 2;-1;0) và có vecto pháp tuyến n (3:5:4)viết phương trình mặt cầu
câu 2 trong không gian với hệ trục tọa độ Oxyz cho mặt cầu (S) có tâm I(2;-3:7) và đi qua điểm M(-4:0;1) viết phương trình mặt cầu
Trong không gian Oxyz, cho hai điểm A(-2;-1;3), B(0;3;1). Gọi ( α ) là mặt phẳng
A. (2;4;1)
B. (1;2;-1)
C. (-1;1;2)
D. (1;0;1)
Trong không gian Oxyz, cho 2 điểm A(2;-1;2), B(0;1;0). Phương trình mặt cầu đường kính AB là A.
(
x
-
1
)
2
+
y
2
+
(
z
-
1
)
2
3
B.
(...
Đọc tiếp
Trong không gian Oxyz, cho 2 điểm A(2;-1;2), B(0;1;0). Phương trình mặt cầu đường kính AB là
A. ( x - 1 ) 2 + y 2 + ( z - 1 ) 2 = 3
B. ( x + 2 ) 2 + ( y - 2 ) 2 + ( z + 2 ) 2 = 2
C. ( x - 1 ) 2 + y 2 + ( z - 1 ) 2 = 3
D. ( x - 1 ) 2 + y 2 + ( z - 1 ) 2 = 12
Trong không gian Oxyz, cho 2 điểm A(2;-1;-3), B(0;3;-1). Phương trình đường kính AB là A.
(
x
+
1
)
2
+
(
y
+
1
)
2
+
(
z
-
2
)...
Đọc tiếp
Trong không gian Oxyz, cho 2 điểm A(2;-1;-3), B(0;3;-1). Phương trình đường kính AB là
A. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 6
B. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 24
C. ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 24
D. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 6
17 tháng 9 2021 lúc 17:07
câu 1: trong không gian với hệ tọa đọ Oxyz, cho 2 điểm a(1,2,-3), b(-2,0,2). tọa độ điểm m thỏa mãn 2ma-mb=0 là?
câu 2: trong khong gian voi he toa do oxyz, cho a(1,-1,2), b(-1,1,-2), c(1,0,c) biet tam giac abc vuong tai a. toa do dinh c la?
1.
Gọi \(M\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y;-3-z\right)\\\overrightarrow{MB}=\left(-2-x;-y;2-z\right)\end{matrix}\right.\)
\(2\overrightarrow{MA}=\overrightarrow{MB}\Rightarrow\left\{{}\begin{matrix}2-2x=-2-x\\4-2y=-y\\-6-2z=2-z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\\z=-8\end{matrix}\right.\) \(\Rightarrow M\left(4;4;-8\right)\)
Đúng 1
Bình luận (0)
2.
Ta có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;2;-4\right)\\\overrightarrow{AC}=\left(0;1;c-2\right)\end{matrix}\right.\)
Tam giác ABC vuông tại A \(\Rightarrow AB\perp AC\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow-2.0+2.1-4\left(c-2\right)=0\)
\(\Rightarrow c=\dfrac{5}{2}\)
Vậy \(C\left(1;0;\dfrac{5}{2}\right)\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho 2 điểm A(3; 2; 1), B(-2; 4; 2). Tìm tọa độ của điểm M thuộc trục hoành và cách đều 2 điểm A,B A.
M
(
-
1
;
0
;
0
)
B.
M
(
-
1
2
;
0
;
0
)
C.
M
(
1
;
0
;
0...
Đọc tiếp
Trong không gian Oxyz, cho 2 điểm A(3; 2; 1), B(-2; 4; 2). Tìm tọa độ của điểm M thuộc trục hoành và cách đều 2 điểm A,B
A. M ( - 1 ; 0 ; 0 )
B. M ( - 1 2 ; 0 ; 0 )
C. M ( 1 ; 0 ; 0 )
D. M ( 1 2 ; 0 ; 0 )
