Trong mặt phẳng xOy cho A(-2;3), B(1;5) , C(3;-7)
a) tìm N thuộc BC : S tam giác ANB= 3S tam gác ANC
b) Tìm P thuộc Ox: PA+PB nhỏ nhất
1. Cho góc xOy = 90 độ và điểm A nằm trong góc xOy gọi B và C là 2 điểm thứ tự trên Ox,Oy ( O,A thuộc nửa mặt phẳng bờ BC ) biết tam giác ABC vuông cân tại A. CMR: OA là phân giác góc xOy
cho 2 góc kề bù xoy và yoz , trong đó xoy =70*
a tính yoz
b trên cùng 1 nửa mặt phẳng bờ chứa tia oy vẽ tia ot sao cho xot =120* .tính yot
a) có \(\widehat{xOy}+\widehat{yOz}=180^o\left(kb\right)\)
\(hay70^o+\widehat{yOz}=180^o\)
\(\Rightarrow\widehat{yOz}=180^o-70^o\)
\(\Rightarrow\widehat{yOz}=110^o\)
b) có \(\widehat{xOy}< \widehat{xOt}\left(70^o< 120^o\right)\)
=> Oy nằm giữa hai tia Ox và Ot
\(\Rightarrow\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
\(hay70^o+\widehat{yOt}=120^o\)
\(\Rightarrow\widehat{yOt}=120^o-70^o\)
\(\Rightarrow\widehat{yOt}=50^o\)
1.cho góc tù xOy. trên nửa mặt phẳng bờ Ox có chứa tia Oy, vẽ tia Ot vuông góc với Ox; trên nửa mặt phẳng bờ Oy có chứa tia Ox, vẽ tia Oz vuông góc với Oy. Gọi Om là tia phân giác của góc xOy.
a) chứng ,imh Om là tia phân giác của góc zOt.
b) tính tổng 2 góc xOy + zOt.
2. cho góc nhọn xOy. trên nửa mặt phẳng bờ Ox không chứa tia Oy. vẽ tia Ot vuông góc với Ox, trên nửa mặt phẳng bờ Oy không chứa tia Ox, vẽ tia Ot vuông gcos với Ox. Gọi Om là tia phân giác của góc xOy.
a) chứng ,imh Om là tia phân giác của góc zOt.
b) tính tổng 2 góc xOy + zOt.
Cho góc vuông xOy và điểm A nằm trong góc xOy. Gọi B và C là 2 điểm lần lượt trên Ox và Oy(O và A là 2 điểm thuộc 2 nửa mặt phẳng bờ BC). Biết tam giác ABC là tam giác vuông cân ở A. Chứng minh rằng OA là tia phân giác của góc xOy.
Trong không gian với hệ tọa độ Descartes Oxyz, cho hai điểm A(3, 2, 1) và B - 1 ; 4 ; - 3 . Điểm M thuộc mặt phẳng (xOy) sao cho M A - M B lớn nhất là
A. M - 5 ; 1 ; 0
B. M(5, 1, 0)
C. M 5 ; - 1 ; 0
D. M - 5 ; - 1 ; 0
Chọn B.
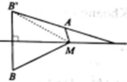
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
![]()
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
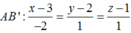
Từ đó tìm được M(5, 1, 0).
Cho xOy là góc tù. Trên nửa mặt phẳng chứa tia Ox có bờ chứa tia Oy, vẽ tia Oý vuông góc Oy, trên nửa mặt phẳng chứa tia Oy có bờ chứa tia Ox. Vẽ Ox’ vuông góc Ox. Chứng minh rằng: a, xOy’ = x’Oy
b, 2 góc xOy và x’Oy’ có cùng tia phân giác
c, 2 góc xOy và x’Oy’ bù nhau
a) Ta có :
xOy' + y'Ox' =90 độ (gt)
y'Ox' + x'Oy = 90 độ (gt)
=> xOy' = 90 - y'Ox'
=> x'Oy = 90 - y'Ox'
=> xOy' = x'Oy (cùng bằng 90 - y'Ox')(dpcm)
b) Gọi Ot là pg y'Ox'(1)
=> y'Ot = x'Ot
tOy = tOx' + x'Oy
Mà y'Ot = tOx'
xOy' = x'Oy (cmt)
=> xOt = tOy
=> Ot là pg xOy (2)
Từ (1) và (2) ta có :
=> y'Ox' và xOy có cùng tia pg
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của A B ⇀ có thể là (với a,b#0)
A. (0;a;b)
B. (a;b;0)
C. (a;0;0)
D. (a;0;b).
trên cùng 1 nửa mặt phẳng bờ chứa tia ox vẽ 2 tia oy ,oz sao cho góc xoy=50 độ ,góc xoz=120 độ .vẽ tia om nằm trong góc xoy sao cho gocs xom=2/3 góc yom . tính góc xom
Cho tia oy nằm giữa 2 tia ox và oy:
a)So sánh góc xoy,yoz với xoz
b)Tìm trong hình vẽ các tia thuộc 2 nửa mặt phẳng
đối nhau có bờ là oy,các tia thuộc cùng một nửa mặt phẳng có bờ oy,các tia thuộc cùng một nửa mặt phẳng có bờ oz
c)Biết xoz=80 độ ,yoz=50 độ.Tính góc xoy
d)Lấy điểm A thuộc tia, điểm Bthuôc tia oz.Tia oy cắt đoạn thẳng AB ở C.Tính AB,biết AC=2cm,CB=3cm
cho goc xoy la goc tu trên nửa mặt phẳng bờ ox chứa oy va oy' sao cho oy' vuông góc với oy', trên nửa mặt phẳng bờ oy chứa ox và ox' sao cho ox' vuông góc với ox hỏi
cm xoy'=yox'
cm xoy và x'oy là 2 góc bù nhau.