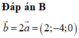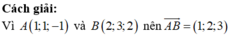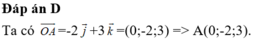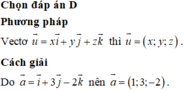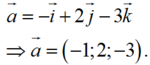Trong không gian với hệ tọa độ Oxyz, cho A(1;0;1) và B(-1;-3) và mặt phẳng \(\left(\alpha\right):x+2y+3z+3=0\), lập phương trình đường thẳng\(\left(\beta\right)\) đi qua 2 điểm A, B và vuông góc với mặt phẳng \(\left(\alpha\right)\)

Những câu hỏi liên quan
#2H3Y1-1~Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A đối xứng với điểm A qua gốc tọa độ O là: A. A(3;-2;1) B. A(3;2;-1) C. A(3;-2;-1) D. A(3;2;1).
Đọc tiếp
#2H3Y1-1~Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với điểm A qua gốc tọa độ O là:
A. A'(3;-2;1)
B. A'(3;2;-1)
C. A'(3;-2;-1)
D. A'(3;2;1).
Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho
a
→
1
;
2
;
3
,
b
→
-
2
;
-
3
;
-
1
. Khi đó
a
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = 1 ; 2 ; 3 , b → = - 2 ; - 3 ; - 1 . Khi đó a → + b → có tọa độ là:
A.(-1;5;2)
B.(3;-1;4)
C.(1;5;2)
D.(1;-5;-2)
Trong không gian với hệ tọa độ Oxyz, cho vectơ
a
→
(
1
;
-
2
;
0
)
và
b
→
2
a
→
Tìm tọa độ của vectơ
b
→
A.
b
→
(
2
;
4
;
2
)
B. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ a → = ( 1 ; - 2 ; 0 ) và b → = 2 a → Tìm tọa độ của vectơ b →
A. b → = ( 2 ; 4 ; 2 )
B. b → = ( 2 ; - 4 ; 2 )
C. b → = ( 3 ; 0 ; 2 )
D. b → = ( 2 ; 4 ; 0 )
Trong không gian với hệ tọa độ Oxyz, cho vectơ
a
→
(
1
;
-
2
;
0
)
v
à
b
→
2
a
→
. Tìm tọa độ của vectơ ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ a → ( 1 ; - 2 ; 0 ) v à b → = 2 a → . Tìm tọa độ của vectơ b →
A. b → =(2;4;2)
B. b → =(2;-4;0)
C. b → =(3;0;2)
D. b → =(2;4;0)
Trong không gian với hệ tọa độ
O
x
y
z
, cho hai điểm
A
(
1
;
1
;
-
1
)
,
B
(
2
;
3
;
2
)
. Vectơ
A
B
→
có tọa độ là A.
(
1
;...
Đọc tiếp
Trong không gian với hệ tọa độ O x y z , cho hai điểm A ( 1 ; 1 ; - 1 ) , B ( 2 ; 3 ; 2 ) . Vectơ A B → có tọa độ là
A. ( 1 ; 2 ; 3 )
B. ( - 1 ; - 2 ; 3 )
C. ( 3 ; 5 ; 1 )
D. ( 3 ; 4 ; 1 )
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)
Trong không gian với hệ tọa độ Oxyz, cho
a
→
-
2
i
→
+
3
j
→
+
k
→
. Tọa độ của
a
→
là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = - 2 i → + 3 j → + k → . Tọa độ của a → là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ . Tìm tọa độ điểm A. A. A(-2;3;0) B. A(-2;0;3) C. A(0;2;-3) D. A(0;-2;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ ![]() . Tìm tọa độ điểm A.
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).
Trong không gian với hệ tọa độ Oxyz, cho
a
→
i
→
+
3
j
→
-
2
k
→
. Tọa độ của vectơ
a
→
là A. (2;-3;-1) B. (-3;2;-1) C. (2;-1;-3) D. (1;3;-2)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = i → + 3 j → - 2 k → . Tọa độ của vectơ a → là
A. (2;-3;-1)
B. (-3;2;-1)
C. (2;-1;-3)
D. (1;3;-2)
Trong không gian với hệ tọa độ Oxyz, cho
a
→
-
i
→
+
2
j
→
-
3
k
→
. Tìm tọa độ của vectơ
a
→
A.
2
,
-
3
,
-
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = - i → + 2 j → - 3 k → . Tìm tọa độ của vectơ a →
A. 2 , - 3 , - 1
B. - 3 ; 2 ; - 1
C. - 1 ; 2 ; - 3
D. 2 ; - 1 ; - 3