Gọi (S) là mặt cầu tâm I (2;1;-1) và tiếp xúc với mặt phẳng (α) có phương trình:
2x – 2y – z + 3 = 0. Bán kính của (S) bằng:
A. 2.
B. 2 9
C. 2 3 .
D. 4 3
Trong không gian tọa độ Oxyz, cho điểm A(1;-2; 3). Gọi (S) là mặt cầu chứa A có tâm I thuộc tia Ox và bán kính bằng 7. Phương trình mặt cầu (S) là:
A . x + 5 2 + y 2 + z 2 = 49
B . x + 7 2 + y 2 + z 2 = 49
C . x - 3 2 + y 2 + z 2 = 49
D . x - 7 2 + y 2 + z 2 = 49
Chọn D
Vì tâm I thuộc tia Ox nên I (m; 0; 0) m > 0
Vì (S) chứa A và có bán kính bằng 7 nên: IA = 7
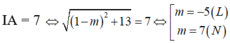
Trong không gian tọa độ Oxyz, cho điểm A (1;-2;3). Gọi (S) là mặt cầu chứa A có tâm I thuộc tia Ox và bán kính bằng 7. Phương trình mặt cầu (S) là:
A. (x+5)²+y²+z²=49.
B. (x+7)²+y²+z²=49.
C. (x-3)²+y²+z²=49.
D. (x-7)²+y²+z²=49.
Chọn D
Vì tâm I thuộc tia Ox nên I (m;0;0) với m>0.
Vì (S) chứa A và có bán kính bằng 7 nên:
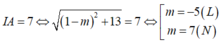
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;6;7) và mặt phẳng ( P ) : x + 2 y + 2 z - 11 = 0 . Gọi (S) là mặt cầu tâm I và tiếp xúc với mặt phẳng (P). Tọa độ tiếp điểm M của mặt phẳng (P) và mặt cầu (S) là
A. (2;3;1)
B. (3;2;1)
C. (1;2;3)
D. (3;1;2)
Chọn C
Tiếp điểm là hình chiếu vuông góc của I lên mặt phẳng (P)
Cho A 1 ; 1 ; 0 ; B - 1 ; 1 ; 0 ; C 1 ; - 1 ; 0 ; D - 1 ; - 1 ; 0 là tâm của 4 mặt cầu có bán kính bằng 1. Gọi I là tâm mặt cầu (S) có bán kính bằng 1 tiếp xúc ngoài với cả 4 mặt cầu kể trên. Tính bán kính R của mặt cầu ngoại tiếp hình chóp I.ABCD.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; -2;3). Gọi (S) là mặt cầu chứa A, có tâm I thuộc tia Ox và bán kính 7. Phương trình mặt cầu (S) là
A. ( x - 3 ) 2 + y 2 + z 2 = 49
B. ( x + 7 ) 2 + y 2 + z 2 = 49
C. ( x - 7 ) 2 + y 2 + z 2 = 49
D. ( x + 5 ) 2 + y 2 + z 2 = 49
Đáp án C
Phương pháp giải: Gọi tọa độ tâm I, vì A thuộc mặt cầu nên IA = R suy ra tọa độ tâm I
Lời giải:
Vì I thuộc tia Ox ![]()
![]()
![]()
Mà A thuộc mặt cầu (S): ![]()
![]()
Vậy phương trình mặt cầu (S) là ( x - 7 ) 2 + y 2 + z 2 = 49
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3). Gọi (S) là mặt cầu chứa A, có tâm I thuộc tia Ox và bán kính 7. Phương trình mặt cầu (S) là
A. x - 3 2 + y 2 + z 2 = 49
B. x + 7 2 + y 2 + z 2 = 49
C. x - 7 2 + y 2 + z 2 = 49
D. x + 5 2 + y 2 + z 2 = 49
Đáp án C
Phương pháp giải: Gọi tọa độ tâm I, vì A thuộc mặt cầu nên IA =R suy ra tọa độ tâm I
Lời giải:
Vì I thuộc tia Ox
![]()
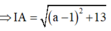
Mà A thuộc mặt cầu (S): R = IA
![]()
Vậy phương trình mặt cầu (S) là x - 7 2 + y 2 + z 2 = 49
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Thể tích của khối nón theo r và h.
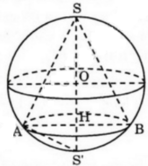
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.

Cho mặt cầu S : x 2 + y 2 + z 2 - 2 m x + 4 m y - 6 ( 1 - m ) z = 0 . Gọi I là tâm (S). Tìm tập hợp điểm I.
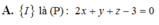
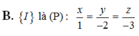
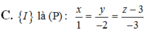
![]()
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Xác định h để thể tích của hình nón là lớn nhất.
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
![]()
![]()
![]()
![]()