Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;0;2) ; N(1;-1;-1) và mặt phẳng (P): x + 2y - z + 2 = 0. Một mặt cầu đi qua M ; N tiếp xúc với mặt phẳng (P) tại điểm E . Biết E luôn thuộc một đường tròn cố định, tính bán kính đường tròn đó.
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A - 1 ; - 4 ; 2 , B 1 ; 0 ; 2 . Trung điểm M của đoạn thẳng AB có tọa độ là
A. M(2;4;0)
B. M(1;2;0)
C. M(0;-1;1)
D. M(0;-2;2)
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B →
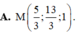
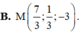
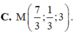
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B → .
A. M 5 3 ; 13 3 ; 1 .
B. M 7 3 ; 1 3 ; - 3 .
C. M 7 3 ; 1 3 ; 3 .
D. M 4 ; - 3 ; 8 .
Trong không gian với hệ tọa độ Oxyz, cho hai điểm: B ( - 1 ; - 1 ; 0 ) , C ( 3 ; 1 ; - 1 ) . Điểm M trên trục Oy cách đều hai điểm B, C có tọa độ là
A. M 0 ; - 9 4 ; 0
B. M 0 ; 4 9 ; 0
C. M 0 ; 0 ; 0
D. M 0 ; 9 4 ; 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm: B(-1;-1;0), C(3;1;-1). Điểm M trên trục Oy cách đều hai điểm B, C có tọa độ là
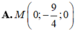
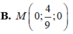
![]()
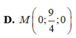
Trong không gian với hệ tọa độ Oxyz cho hai điểm A - 1 ; - 1 ; 0 , B 3 ; 1 ; - 1 . Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:
A. M 0 ; 9 2 ; 0
B. M 0 ; 9 4 ; 0
C. M 0 ; - 9 4 ; 0
D. M 0 ; - 9 2 ; 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M( 1; -1; -2), N(3; 5; 7). Tính tọa độ của véc tơ M N → .
A. M N → = ( 2 ; 9 ; 6 )
B. M N → = ( 2 ; 6 ; 9 )
C. M N → = ( 6 ; 2 ; 9 )
D. M N → = ( 6 ; 2 ; - 9 )
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(-1;-1;0), B(3;1;-1). Điểm M thuộc trục Oy và cách đều hai điểm A, B có tọa độ là:

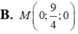
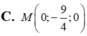

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-1 ;2 ;3) và B(3 ;-1 ;2). Điểm M thỏa mãn M A . M A → = 4 M B . M B → có tọa độ là:
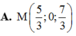
![]()
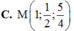
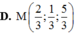
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 1 ; 1 , B 2 ; 0 ; - 1 . Điểm M trong không gian thỏa mãn M A = 2 M B . Khi đó độ dài OM nhỏ nhất bằng
A. 17 - 2 3
B. 19 + 2 3
C. 19 - 2 3
D. 2 3