Cho hình vuông ABCD có điểm M(1;2) là trung điểm AB, N có tọa độ (2;-1) là điểm thuộc cạnh AC sao cho AN=3NC. Viết phương trình đường thẳng CD

Những câu hỏi liên quan
Cho hình vuông có cạnh bằng 15cm. Trên cạnh AB lấy điểm M sao cho diện tích
tam giác AMD bằng 1/3 diện tích hình vuông ABCD
Yêu cầu đề bài là gì vậy bạn? Nếu là tìm diện tích tam giác $AMD$ thì:
$S_{AMD}=\frac{1}{3}S_{ABCD}=\frac{1}{3}.15.15=75$ (cm2)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng
3
4
diện tích vuông ABCD A. Điểm E ở trên cạnh AB sao cho BE 8 m B. Điểm E ở trên cạnh AB sao cho BE 6 m C. Điểm E ở trên cạnh AB sao cho BE 12 m D. Điểm E là trung điểm của AB
Đọc tiếp
Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng 3 4 diện tích vuông ABCD
A. Điểm E ở trên cạnh AB sao cho BE = 8 m
B. Điểm E ở trên cạnh AB sao cho BE = 6 m
C. Điểm E ở trên cạnh AB sao cho BE = 12 m
D. Điểm E là trung điểm của AB
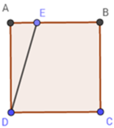
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
1. Cho tứ diện ABCD có AD vuông góc (ABC), AD=a√3. Góc giữa (ABC) và (DBC) bằng 60⁰. Gọi M là trung điểm AD. Tính khoảng cách từ M đến (BCD). 2. Cho hình chóp S.ABCD có SA vuông góc (ABCD), đáy ABCD là hình chữ nhật tâm O. Biết AD=2a, SA=a. Khoảng cách từ O đến (SCD) bằng
1) cho hình thang ABCD có AB//CD;AB>CD;AC vuông góc với BD.Trên cạnh đáy AB lấy điểm M sao cho AM bằng độ dài đường trung bình của hình thang ABCD .CM:AC là tia phân giác góc A
2)Cho hình thang ABCD có góc A=góc B=90 độ ;BC=2AD=2AB .Gọi M là 1 điểm trên đáy nhỏ AB kẻ Mx vuông với MB .Mx cắt CD tại N.CM:MB=MN
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)
CHO HÌNH VUÔNG abcd có AB = 6cm ; m là trung điểm của BCdn = 1/2nc.Tính diện tích hình tam gác AMN
Cho 2018 điểm phân biệt M1,M2,......,M2018 trên mựt phẳng , vẽ một hình vuông ABCD có cacnhj bằng 2. Chứng minh rằng tồn tại vô số điểm I nằm trên cạnh hình vuông ABCD sao cho: \(IM_1+IM_2+............+IM_{2018}\ge2018\)
Cho hình vuông ABCD có cạnh 4cm.Trên các cạnh của hình vuông lấy lần lượt các trung điểm M,N,P,Q.Nối 4 điểm đó để được hình tứ giác MNPQ.Tính tỉ số giữa diện tích hình tứ giác MNPQ và hình vuông ABCD
cho hình vuông abcd có cạnh 4cm trên các cạnh của hình vuông lấy lần lượt các trung điểm m,n,p,q.Nối 4 điểm đó để được hình tứ giác mnpq.Tính tỉ số của diện tích hình tứ giác mnpq và hình vuông abcd.
Cho hình vuông ABCD có cạnh 4cm.Trên các cạnh của hình vuông lấy lần lượt các trung điểm M,N,P,Q. Nối bốn điểm đó để được hình tứ giác MNPQ.Tính tỉ số diện tích của hình tứ giác MNPQ và hình vuông ABCD

















