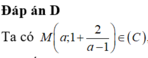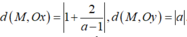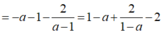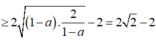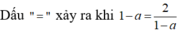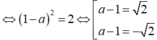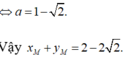1) Điểm M (xM ; yM ) thuộc đường thẳng y=2x-1 và cách trục tung một khoảng bằng 6 . Tìm tọa độ của M
Những câu hỏi liên quan
Cho hàm số y=5x
a) Vẽ đồ thị hàm số
b) Biết rằng điểm A(xm,ym) là 1 điểm thuộc đồ thị hàm số. Tính m
c) Gọi M(xm,ym) là 1 điểm thuộc đồ thị hàm số, Tìm tọa độ điểm M biết 5xm+ym=10
cho điểm M(1-2t; 1+t) tìm M sao cho xM^2+yM^2 nhỏ nhất
\(A=x_M^2+y_M^2=\left(1-2t\right)^2+\left(1+t\right)^2\)
\(A=5t^2-2t+2=5\left(t-\frac{1}{5}\right)^2+\frac{9}{5}\ge\frac{9}{5}\)
\(A_{min}=\frac{9}{5}\) khi \(t=\frac{1}{5}\Rightarrow M\left(\frac{3}{5};\frac{6}{5}\right)\)
Cho hàm số
y
x
+
1
x
-
1
có đồ thị là (C). Gọi
M
(
x
M
;
y
M
)
là một điểm bất kỳ...
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị là (C). Gọi M ( x M ; y M ) là một điểm bất kỳ trên (C). Khi tổng khoảng cách từ M đến hai trục tọa độ là nhỏ nhất, tính tổng x M + y M .
A. 
B. 
C. 
.
D. 
Cho hàm số
y
x
3
-
3
x
2
+
1
có đồ thị (C) và điểm A(1;-1). Xét điểm M bất kì trên (C) có
x
M
m
(
m
≠
1
)
. Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B.
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 1 có đồ thị (C) và điểm A(1;-1). Xét điểm M bất kì trên (C) có x M = m ( m ≠ 1 ) . Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B.
Biết đồ thị
(
C
m
)
của hàm số luôn luôn đi qua một điểm M
M
(
x
m
;
y
m
)
cố định khi m thay đổi, khi đó
x
m
+
y
m
bằng A.-1 B.-3 C.1 D.-2
Đọc tiếp
Biết đồ thị
(
C
m
)
của hàm số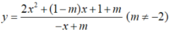 
luôn luôn đi qua một điểm M
M
(
x
m
;
y
m
)
cố định khi m thay đổi, khi đó
x
m
+
y
m
bằng
A.-1
B.-3
C.1
D.-2
Đáp án C
Gọi 
là điểm cố định cần tìm.
Ta có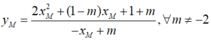 
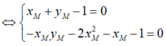
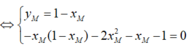
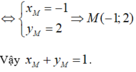
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
x
2
+
1
có đồ thị (C) và điểm A(1;-1). Xét điểm M bất kì trên (C) có
x
M
m
m
≠
1
. Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B. A. - 2 – m B.
-
m...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 1 có đồ thị (C) và điểm A(1;-1). Xét điểm M bất kì trên (C) có x M = m m ≠ 1 . Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B.
A. - 2 – m
B. - m 3 + 3 m 2 + 1
C. 2 – m
D. - m 3 + 3 m 2 - 3
Cho hàm số
y
1
4
x
4
-
8
x
2
-
4
có đồ thị (C). Biết điểm
M
∈
(
C
)
sao cho
x
M
0
và
x
M
là nghiệm của phương trình y-4. Phương trình tiếp tuyến của (C) tại điểm M là: A. y24x+16. B. y-24x+16. C. y-24x-...
Đọc tiếp
Cho hàm số y = 1 4 x 4 - 8 x 2 - 4 có đồ thị (C). Biết điểm M ∈ ( C ) sao cho x M < 0 và x M là nghiệm của phương trình y''=-4. Phương trình tiếp tuyến của (C) tại điểm M là:
A. y=24x+16.
B. y=-24x+16.
C. y=-24x-80.
D. y=24x-80.
Cho hàm số
y
1
4
x
4
-
8
x
2
-
4
có đồ thị (C). Biết điểm
M
∈
C
sao cho
x
M
0
và
x
M
là nghiệm của phương trình
y
-
4
. Phương trình...
Đọc tiếp
Cho hàm số y = 1 4 x 4 - 8 x 2 - 4 có đồ thị (C). Biết điểm M ∈ C sao cho x M < 0 và x M là nghiệm của phương trình y " = - 4 . Phương trình tiếp tuyến của (C) tại điểm M là:
A. y = 24 x + 16
B. y = - 24 x + 16
C. y = - 24 x - 80
D. y = 24 x - 80
Cho hàm số
y
3
x
+
6
x
-
1
có đồ thị (C) và điểm A(1;3) . Xét điểm M bất kì trên (C) có
x
M
m
m
≠
1
. Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B. A. 3-m B. ...
Đọc tiếp
Cho hàm số y = 3 x + 6 x - 1 có đồ thị (C) và điểm A(1;3) . Xét điểm M bất kì trên (C) có x M = m m ≠ 1 . Đường thẳng MA cắt (C) tại điểm B (khác M). Tìm tung độ của điểm B.
A. 3-m
B. 3 m - 1
C. 3 m - 12 m - 1
D. 2-m
