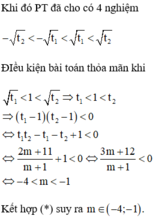Cho bốn số x1, x2, x3, x4 khác 0 thỏa mãn x22 = x1.x3 ; x23 = x2.x4 Chứng minh rằng: x1/ x4 = (x1 x2 x3 / x2 x3 x4 ) ^3

Những câu hỏi liên quan
1. cho 6 số khác 0 x1,x2,x3,x4,x5,x6 thỏa mãn điều kiện
x2 mũ 3 = x1.x3, x3 mũ 2 =x2.x4
x4 mũ 2 = x3.x5 , x5 mũ 2 = x4.x6
Cho các số tự nhiên x1,x2,..,x101x1,x2,..,x101 thỏa mãn x1+x2+x3+x4+...+x99+x100+x101=0x1+x2+x3+x4+...+x99+x100+x101=0 và x1+x2=x3+x4=...=x97+x98=x99+x100=x100+x101=1.x1+x2=x3+x4=...=x97+x98=x99+x100=x100+x101=1. Số nguyên x100x100 bằng bao nhiêu ?
Cho sáu số khác 0:x1;x2;x3;x4;x5;x6 thoả mãn các điều kiện: x22=x1x3 x32=x2x1 x42=x3x5 x52=x4x6 CMR:
x1/x6=[x1+...+x/x2+....+x6]^5
Cho x1, x2, x3, x4, x5, x6 là các số đôi một khác nhau thuộc tập {1, 2, 3, 4, 5, 6} và thỏa mãn x1-5x2+10x3-10x4+5x5-x6=0. Hỏi có bao nhiêu cách chọn bộ (x1, x2, x3, x4, x5, x6)?
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
y
m
+
1
x
4
-
2
2
m
-
3
x
2
+
6
m
+
5
cắt trục hoành tại bốn điểm phân biệt có các hoành độ
x
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = m + 1 x 4 - 2 2 m - 3 x 2 + 6 m + 5 cắt trục hoành tại bốn điểm phân biệt có các hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 < x 2 < x 3 < 1 < x 4
A. m ∈ - 1 ; - 5 6
B. m ∈ - 3 ; - 1
C. m ∈ - 3 ; 1
D. m ∈ - 4 ; - 1
cho 5 số:x1,x2,x3,x4,x5 mỗi số =1 hoặc = -1.Chứng minh: x1.x2+x2.x3+x3.x4+x4.x5+x5.x1 khác 0
x1;x2;x3;x4;x5=-1 hoặc 1
=>x1.x2;x2.x3;x3.x4;x4.x5;x5.x1 bằng 1 hoặc -1
giả sử x1.x2+x2.x3+x3.x4+x4.x5+x5.x1=0
=>số các số hạng 1 và -1 bằng nhau
=>số các số hạng chia hết cho 2
=>5 chia hết cho 2(có 5 số hạng) Vô lí
=>x1.x2+x2.x3+x3.x4+x4.x5+x5.x1\(\ne0\)
=>đpcm
Đúng 0
Bình luận (0)
chtt
ai làm ơn tích mình ,mình tích lại cho
Đúng 0
Bình luận (0)
x1x2+x2x3+x3x4+x4x5+x5x1=[(x2)*2]+[(x2)*6]+[(x2)*12]+[(x2)*20]+[(x2)*5]=(x2)*(2+6+12+20+5)
Mà x2 là số dương và 2+6+12+20+5 cũng là số dương nên x1x2+x2x3+x3x4+x4x5+x5x1 khác 0
tick nha
Đúng 0
Bình luận (0)
Bài 1 : Cho a,b,c là các số hữu tỉ khác 0 sao cho a+b-c/c=a-b+c/b=(-a)+b+c/a
Tính giá trị của biểu thức A=(a+b).(b+c).(c+a)/abc
(LƯU Ý : DẤU / LÀ ...TRÊN.....)
Bài 2 : Cho x,x2,x3,x4,x5,x6 thỏa mãn :
(x2)^2=x1.x3
(x3)^2=x2.x4
(x4)^2=x3.x5
(x5)^2=x4.x6
Chứng minh rằng : x1/x6=(x1+x2+x3+x4+x5/x2+x3+x4+x5+x6)^5
Giusp mk vs nhé các bn !!!
Tìm m để phương trình x^4-2(m+1)x^2+m+5=0 có 4 nghiệm thỏa mãn x1<x2<x3<x4;x1-x2=x2-x3=x3-x4
Đặt x2−2x+m=tx2−2x+m=t, phương trình trở thành t2−2t+m=xt2−2t+m=x
Ta có hệ {x2−2x+m=tt2−2t+m=x{x2−2x+m=tt2−2t+m=x
⇒(x−t)(x+t−1)=0⇒(x−t)(x+t−1)=0
⇔[x=tx=1−t⇔[x=tx=1−t
⇔[x=x2−2x+mx=1−x2+2x−m⇔[x=x2−2x+mx=1−x2+2x−m
⇔[m=−x2+3xm=−x2+x+1⇔[m=−x2+3xm=−x2+x+1
Phương trình hoành độ giao điểm của y=−x2+x+1y=−x2+x+1 và y=−x2+3xy=−x2+3x:
−x2+x+1=−x2+3x−x2+x+1=−x2+3x
⇔x=12⇒y=54⇔x=12⇒y=54
Đồ thị hàm số y=−x2+3xy=−x2+3x và y=−x2+x+1y=−x2+x+1:
Cho các số X1 , X2 , X3 , X4 thỏa mãn :
\(\frac{X1-1}{3}=\frac{X2-2}{2}=\frac{X3-3}{1}\)
Và X1 + X2 + X3 = 30
Bỏ x4 đi nhé bn
Theo t/c dãy tỉ số=nhau:
\(\frac{x_1-1}{3}=\frac{x_2-2}{2}=\frac{x_3-3}{1}=\frac{x_1-1+x_2-2+x_3-3}{3+2+1}\)\(=\frac{\left(x_1+x_2+x_3\right)-\left(1+2+3\right)}{6}=\frac{30-6}{6}=\frac{24}{6}=4\)
=>x1-1=4.3=12=>x1=13
x2-2=4.2=8=>x2=10
x3-3=4=>x3=7
Đúng 0
Bình luận (0)
Uk mik cảm ơn trong lúc chờ bạn thì mik giải được rồi nhưng dù sao cũng cảm ơn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời