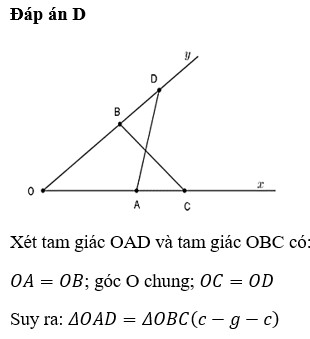
Cho góc xOy nhọn, trên tia Ox lấy điểm A và C ( C nằm giữa O và A ) ; trên tia Oy lấy điểm B và D ( B nằm giữa O và D ) sao cho OA=OB. AB và CD cắt nhau tại I. Đường thẳng vuông góc với CD tại I cắt tia phân giác của góc xOy tại H. Chứng minh CH=DH.

Những câu hỏi liên quan
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OAOB; OCOD; (A nằm giữa O và C; B nằm giữa O và D) A.
∆
O
A
D
∆
O
C
B
B.
∆
O
D
A
∆
O
B
C
C.
∆
A
O
D
∆
B
C
O
D.
∆
O
A
D...
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA=OB; OC=OD; (A nằm giữa O và C; B nằm giữa O và D)
A. ∆ O A D = ∆ O C B
B. ∆ O D A = ∆ O B C
C. ∆ A O D = ∆ B C O
D. ∆ O A D = ∆ O B C
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA OB; OC OD (A nằm giữa O và C; B nằm giữa O và D) So sánh hai góc
C
A
D
^
và
C
B
D
^
A.
C
B
D
^
C...
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D) So sánh hai góc C A D ^ và C B D ^
A. C B D ^ = C A D ^
B. C B D ^ < C A D ^
C. C B D ^ > C A D ^
D. C B D ^ = 2. C A D ^
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OAOB; OCOD (A nằm giữa O và C; B nằm giữa O và D). So sánh hai góc CAD và góc CBD A.
C
B
D
^
C
A
D
^
B.
C
B
D
^...
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA=OB; OC=OD (A nằm giữa O và C; B nằm giữa O và D). So sánh hai góc CAD và góc CBD
A. C B D ^ = C A D ^
B. C B D ^ < C A D ^
C. C B D ^ > C A D ^
D. C B D ^ = 2 C A D ^
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA OB; OC OD (A nằm giữa O và C; B nằm giữa O và D) Chọn câu đúng A.
Δ
O
A
D
Δ
O
C
B
B.
Δ
O
D
A
Δ
O
B
C
C.
Δ
A
O
D
Δ
B
C
O
D.
Δ
O...
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D) Chọn câu đúng
A. Δ O A D = Δ O C B
B. Δ O D A = Δ O B C
C. Δ A O D = Δ B C O
D. Δ O A D = Δ O B C
Cho góc nhọn xOy trên tia Ox lấy 2 điểm A và B sao cho A nằm giữa O và B . Trên tia Oy sao cho C nằm giữa O và D. CM rằng AB+CD
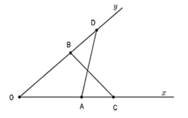
5. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB ; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).
a. Chứng minh DOAD = DOBC
b. So sánh 2 góc CAD và CBD .
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Đúng 0
Bình luận (0)
Cho góc nhọn xoy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OD. (A nằm giữa O và B; B nằm giữa O và D)
A. Chứng minh ∆OAD = ∆OBC
B. So sánh 2 góc CAD VÀ CBD
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D). So sánh hai góc CAD và CBD.
a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )
Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA OB; OC OD. (A nằm giữa O và C; B nằm giữa O và D).a. Chứng minh ∆OAD ∆OBCb. So sánh 2 góc CAD và CBD.(có hình giúp mình ạ) Cảm ơn!
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).
a. Chứng minh ∆OAD = ∆OBC
b. So sánh 2 góc CAD và CBD.
(có hình giúp mình ạ) Cảm ơn!
a) Xét ΔOAD và ΔOBC có:
OA = OB (gt)
góc COD chung
OD = OC (gt)
suy ra ΔOAD = ΔOBC (cgc)
b) suy ra góc OAD = góc OBC (2 góc tương ứng)
Có góc OAD + góc OAC = 180 độ
góc OBC + góc CBD = 180 độ
mà góc OAD = góc OBC (cmt)
suy ra góc OAC = góc CBD (đpcm)
Đúng 0
Bình luận (0)