Cho n điểm phân biệt (n ≥ 2; n ∈ N) trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong n điểm đó. Có tất cả 28 đoạn thẳng. Hãy tìm n.
A. n = 9
B. n = 7
C. n = 8
D. n = 6
Trong mặt phẳng cho n điển phân biệt. Cứ 2 điểm trong n điểm đó vẽ được một đoạn thẳng, tổng số đoạn thẳng vẽ được là 2021055. Tính số n điểm phân biệt
ai biết thí giúp mình với mình k cho
n * (n - 1) : 2 =2021055
n * ( n - 1 ) =4042110
n * ( n - 1 ) = 2010 * 2011
n = 2011
vậy có tất cả 2011 điểm phân biệt
1.Hỏi qua n điểm phân biệt có bao nhiêu đoạn thẳng biết cứ qua 2 điểm ta vẽ được 1 đoạn thẳng .
2.Cho n điểm phân biệt (n> hoặc = 2; n thuộc N) cứ qua 2 điểm vẽ được 1 đoạn thẳng , và qua n điểm vẽ được tất cả 300 đoạn thẳng. Hỏi n=?
Cho n điểm phân biệt trong đó không có bộ ba điểm nào thẳng hàng . Qua 2 điểm phân biệt ta vẽ được 1 đường thẳng . Biết rằng vẽ được tất cả 2415 đưởng thẳng từ n điểm đã cho . Tìm n ( n >10 )
Cho n điểm phân biệt (n thuộc N, n nhỏ hơn hoặc bằng 2.Trong đó không có 3 điểm nào thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm. Hỏi có bao nhiêu đường thẳng phân biệt?
ta có qua 2 điểm ta vẽ được 1 đường thẳng
3điểm ta vẽ được 2đương thẳng
n điểm ta vẽ được n(n-1):2 đường thẳng
cho 100 điểm phân biệt trong đó có đúng n điểm thẳng hàng, qua 2 điểm phân biệt ta kẻ được một đường thẳng.Tìm n để số đường thẳng kẻ được bằng 4915
- Nếu trong n điểm không có 3 điểm nào thẳng hàng thì số đường thẳng kẻ được là \(\dfrac{n\left(n-1\right)}{2}\) đường.
- Số đường thẳng bị giảm nếu n điểm trong đó không có 3 điểm nào thẳng hàng trở thành n điểm thẳng hàng là: \(\dfrac{n\left(n-1\right)}{2}-1\) đường.
- Số đường thẳng tạo bởi 100 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng là: \(\dfrac{100.99}{2}=4950\) đường.
- Theo đề bài ta có: \(4950-\left(\dfrac{n\left(n-1\right)}{2}-1\right)=4915\)
\(\Leftrightarrow n\left(n-1\right)=72\)
\(\Leftrightarrow n^2-n-72=0\)
Giải phương trình trên ta được \(n=9\left(n\right)\) hay \(n=-8\) (loại)
Vậy n=9.
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n ≥ 2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 20
B. 21
C. 30
D. 32
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d1 và hai đỉnh thuộc d2. Loại này có ![]() tam giác.
tam giác.
Loại 2: Tam giác có một đỉnh thuộc d2 và hai đỉnh thuộc d1. Loại này có ![]() tam giác.
tam giác.
Theo bài ra ta có: ![]()
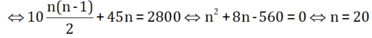
Chọn A.
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt ( n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 16
B. 21
C. 30
D. 20
Tam giác cần lập thuộc hai loại
Loại 1: Tam giác có một đỉnh thuộc d 1 và hai đỉnh thuộc d 2 .
Loại này có C 10 1 . C n 2 tam giác.
Loại 2: Tam giác có một đỉnh thuộc d 2 và hai đỉnh thuộc d 1 .
Loại này có C 10 2 . C n 1 tam giác.
Theo bài ra ta có: C 10 1 . C n 2 + C 10 2 . C n 1 = 2800
⇔ 10 n ( n − 1 ) 2 + 45 n = 2800 ⇔ n 2 + 8 n − 560 = 0 ⇔ n = 20
Chọn đáp án D
Cho n điểm phân biệt [n thuộc N,n lớn hơn hoặc bằng 2] trongđó không có 3 điểm nào thẳng hàng,kẻ các đường thẳng đi qua các cặp điểm.Hỏi có bao nhiêu đường thẳng phân biệt.
Gọi n điểm đã cho là: \(A_1;A_2;A_3;...;A_n\); n\(\ge\)2.
Vì không có 3 điểm nào thẳng hàng nên :
+) Nối \(A_1\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_2\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
...
+) Nối \(A_3\) với ( n - 1) điểm còn lại ta có: ( n - 1) đường thẳng.
Như chúng ta có: n ( n - 1) đường thẳng
Tuy nhiên mỗi đường thẳng được tính 2 lần ( VD như nối \(A_1\)với \(A_2\)ta có đường thẳng \(A_1\)\(A_2\); còn nối \(A_2\)với \(A_1\)ta có đường thẳng \(A_2\)\(A_1\); và 2 đường thẳng \(A_1\)\(A_2\); \(A_2\)\(A_1\) trùng nhau )
=> Do đó số đường thẳng phân biệt là: n ( n - 1) : 2.
Cho N điểm phân biệt A1,A2,A3,....An. Trong đó không có 3 điểm bất kì nào thẳng hàng. Hỏi qua 2 điểm trong N điểm trên vẽ được bao nhiêu đường thẳng phân biệt
Ta thấy: Trong n điểm phân biệt cho trước, cứ qua 1 điểm ta vẽ được n - 1 đường thẳng. Vậy qua n điểm ta vẽ được n(n - 1) đoạn thẳng.
Nhưng nếu tính vậy thì mỗi đường thẳng sẽ bị tính đi tính lại 2 lần
Vậy số đoạn thẳng phân biệt được tạo ra từ n điểm phân biệt trên là: \(\frac{n\left(n-1\right)}{2}\)(đường thẳng)