
Những câu hỏi liên quan
Câu 9. [VDC] Cho hai đường tròn bằng nhau (O; R) và (O/; R) cắt nhau tại A và B sao cho tâm đường tròn này nằm trên đường tròn kia. Tính theo R diện tích tứ giác OAO/BA.R bình phương căn 3 trên 2 B.R bình phương căn 3 trên 3 C.R bình phương căn 5 trên 2 D.R bình phương căn 5 Câu 10. [VDC] Cho tam giác đều ABC có cạnh bằng 7 cm. Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và bán kínhđường tròn nội tiếp tam giác ABC (như hình vẽ). Tổng R + r bằngA. 21 c...
Đọc tiếp
Câu 9. [VDC] Cho hai đường tròn bằng nhau (O; R) và (O/; R) cắt nhau tại A và B sao cho tâm đường tròn này nằm trên đường tròn kia. Tính theo R diện tích tứ giác OAO/B
A.R bình phương căn 3 trên 2 B.R bình phương căn 3 trên 3 C.R bình phương căn 5 trên 2 D.R bình phương căn 5
Câu 10. [VDC] Cho tam giác đều ABC có cạnh bằng 7 cm.
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và bán kính
đường tròn nội tiếp tam giác ABC (như hình vẽ). Tổng R + r bằng
A. "21 căn 3 trên 2" cm. B. "7 căn 3 trên 6"cm.
C. "7căn 3 trên 2"cm. D. "7căn 3 trên 3"cm.
Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI HI.giúp e với ạ e tra mạng có phần e chưa hiểu lắm
Đọc tiếp
Câu 9: (1,0 điểm) Cho đường tròn (O), đường kính AB. Lấy điểm C nằm trên đường tròn (C ≠ A, C ≠ B). Các tiếp tuyến của đường tròn (O) tại A và C cắt nhau tại D. Gọi H là hình chiếu vuông góc của C trên đường thẳng AB. I là giao điểm của BD và CH. Chứng minh rằng CI = HI.
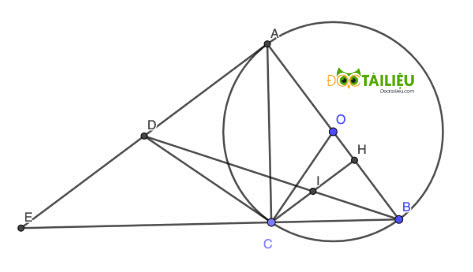
giúp e với ạ e tra mạng có phần e chưa hiểu lắm
DA,DC là tiếp tuyến của (O)
=>DA=DC
=>OD vuông góc AC
CH vuông góc AB
=>AD//CH
=>CI/AD=IM/MD
IH/AD=BI/BD
mà IM/MD=BI/BD
nên CI/AD=IH/AD
=>CI=IH
Đúng 0
Bình luận (0)
Câu 9. Cho một đường thăng d cô định nằm ngoài đường tròn (O; R) Gọi A là một điểm di động trên d. Kẻ các tiếp tuyến AB, AC với đường tròn (O) (với B, C là các tiếp điểm). OA cắt cung nhỏ BC tại I. a) Chứng minh i là tâm đường tròn nội tiếp ABC
Ta có: \(OB=OC=R\) ; \(AB=AC\) (t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là trung trực của BC
\(\Rightarrow OA\) là phân giác góc \(\widehat{BAC}\) (1)
Mặt khác I thuộc OA \(\Rightarrow IB=IC\Rightarrow\Delta IBC\) cân tại I
\(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
Mà \(\widehat{BCI}=\widehat{ABI}\) (góc nội tiếp và góc tiếp tuyến cùng chắn cung BI)
\(\Rightarrow\widehat{CBI}=\widehat{ABI}\Rightarrow BI\) là phân giác \(\widehat{ABC}\) (2)
(1);(2) \(\Rightarrow I\) là tâm đường tròn nội tiếp tam giác ABC
Đúng 2
Bình luận (1)
Câu 3: Trang 131 sách VNEN 9 tập 1
Cho hai đường tròn (O; R) và (O; R) cắt nhau tại A và B (R R). Gọi M là trung điểm của OO. Kẻ đường thẳng vuông góc với MA tại A, đường thẳng này cắt các đường tròn (O; R) và (O; R) theo thứ tự tại C và D (khác A).
a) Chứng minh rằng AC AD.
b) Lấy K sao cho M là trung điểm của AK. Chứng minh rằng KB vuông góc với AB.
c) Kẻ đường kính AE của đường tròn (O) và đường kính AF của (O). Chứng minh rằng bốn điểm E, K, B, F thẳng hàng và OO song song với EF.
d)...
Đọc tiếp
Câu 3: Trang 131 sách VNEN 9 tập 1 Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại A và B (R > R'). Gọi M là trung điểm của OO'. Kẻ đường thẳng vuông góc với MA tại A, đường thẳng này cắt các đường tròn (O; R) và (O'; R') theo thứ tự tại C và D (khác A). a) Chứng minh rằng AC = AD. b) Lấy K sao cho M là trung điểm của AK. Chứng minh rằng KB vuông góc với AB. c) Kẻ đường kính AE của đường tròn (O) và đường kính AF của (O'). Chứng minh rằng bốn điểm E, K, B, F thẳng hàng và OO' song song với EF. d) Chứng minh K là trung điểm của EF.
Câu 5:Với 5_x_13 , giá trị lớn nhất của biểu thức A sqrt{x-5}+sqrt{13-x} là ....Câu 6:Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) ..../.....Câu 8Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Axtrên Ax lấy điểm B sao cho OB10 cm.Khi đó AB .... cm.Câu 9:Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt A...
Đọc tiếp
Câu 5:
Với 5<_x<_13 , giá trị lớn nhất của biểu thức A =\(\sqrt{x-5}+\sqrt{13-x}\) là ....
Câu 6:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) = ..../.....
Câu 8
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= .... cm.
Câu 9:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.
Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại E và F.
Khi đó góc EFO = ... độ.
câu 5: Amax=4
câu 6: 0/7
câu 8:ab=8
caau9: 90 độ
Đúng 0
Bình luận (0)
Câu 5:Với 5_x_13 , giá trị lớn nhất của biểu thức A sqrt{x-5}+sqrt{13-x} là ....Câu 6:Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) ..../.....Câu 8Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Axtrên Ax lấy điểm B sao cho OB10 cm.Khi đó AB .... cm.Câu 9:Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt A...
Đọc tiếp
Câu 5:
Với 5<_x<_13 , giá trị lớn nhất của biểu thức A =\(\sqrt{x-5}+\sqrt{13-x}\) là ....
Câu 6:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) = ..../.....
Câu 8
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= .... cm.
Câu 9:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.
Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại E và F.
Khi đó góc EFO = ... độ.
(mọi người giải giúp tôi với )
Câu 5:Với 5_x_13 , giá trị lớn nhất của biểu thức A sqrt{x-5}+sqrt{13-x} là ....Câu 6:Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) ..../.....Câu 8Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Axtrên Ax lấy điểm B sao cho OB10 cm.Khi đó AB .... cm.Câu 9:Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt A...
Đọc tiếp
Câu 5:
Với 5<_x<_13 , giá trị lớn nhất của biểu thức A =\(\sqrt{x-5}+\sqrt{13-x}\) là ....
Câu 6:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) = ..../.....
Câu 8
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= .... cm.
Câu 9:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.
Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại E và F.
Khi đó góc EFO = ... độ.
(mọi người giải giúp tôi với )
Câu 5:Với 5_x_13 , giá trị lớn nhất của biểu thức A sqrt{x-5}+sqrt{13-x} là ....Câu 6:Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) ..../.....Câu 8Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Axtrên Ax lấy điểm B sao cho OB10 cm.Khi đó AB .... cm.Câu 9:Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt A...
Đọc tiếp
Câu 5:
Với 5<_x<_13 , giá trị lớn nhất của biểu thức A =\(\sqrt{x-5}+\sqrt{13-x}\) là ....
Câu 6:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) = ..../.....
Câu 8
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= .... cm.
Câu 9:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.
Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại E và F.
Khi đó góc EFO = ... độ.
Câu 5:Với 5_x_13 , giá trị lớn nhất của biểu thức A sqrt{x-5}+sqrt{13-x} là ....Câu 6:Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) ..../.....Câu 8Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Axtrên Ax lấy điểm B sao cho OB10 cm.Khi đó AB .... cm.Câu 9:Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt A...
Đọc tiếp
Câu 5:
Với 5<_x<_13 , giá trị lớn nhất của biểu thức A =\(\sqrt{x-5}+\sqrt{13-x}\) là ....
Câu 6:
Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy( a;b) = ..../.....
Câu 8
Cho đường tròn (O;6cm) và điểm A nằm trên đường tròn.Qua A kẻ tiếp tuyến Ax
trên Ax lấy điểm B sao cho OB=10 cm.Khi đó AB= .... cm.
Câu 9:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn.
Gọi M là điểm bất kỳ thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By tại E và F.
Khi đó góc EFO = ... độ.
(mọi người giải giúp tôi với )
câu 5: 4
câu 6 0/7
câu 8: 8
câu 9: 90
Đúng 0
Bình luận (0)
111111111111111111111111111111111111111111111111111111111111111111111
Đúng 0
Bình luận (0)











