(Các bạn chỉ cần làm ý c thôi nha)
Cho hình vuông ABCD. Gọi M là trung điểm AB; N là trung điểm CD.
a) Tứ giác BMDN là hình gì? Vì sao?
b) CM: \(S_{ADM}=\dfrac{1}{4}.S_{ABCD}\)
c) Gọi trung điểm BC là P, AP cắt BN tại I. Chứng minh: DI=AB
cho hình chữ nhật ABCD từ đỉnh B kẻ BH vuông góc với AC, gọi M,N,P,Q lần lượt là trung điểm của AH, AB, NC, DC
a, Chứng minh MN = 1/2 BH
b, Chứng minh BM vuông góc với MQ
Mình không cần hình các bạn nhé chỉ cần cách giải thôi bạn nào làm được ý b mà đúng thì mình cảm ơn nhiều
Cho hình vuông ABCD. Gọi M,N lần lượt là trung điểm của AB, CD. Gọi H là hình chiếu của D lên MC.
a) Chứng minh Ac,MN,Bd đồng quy
b) Chứng minh AH\(⊥\)HN
c)Gọi K là giao điểm của DH và BC. Chứng minh Hb là tia phân giác của \(\widehat{MHK}\)
CÁC BẠN CHỈ CẦN LÀM GIÙM MÌNH CÂU C THÔI
Mong các bạn giúp mình
Cho tam giác ABC vuông tại A(AB<AC), M là trung điểm cạnh BC . MD vuông góc với AB ; ME vuông góc với AC . Trên tia đối DM lấy điểm N sao cho DN=DM
a) chứng minh AMBN là hình thoi
b) CK vuông góc với BN , I là giao điểm của AM và DE . Chứng minh tam giác IKN cân
c) Gọi F là giao điểm của AM và CD . Chứng minh AN=3MF
Chỉ cần làm ý b với ý c thôi
Cho hình bình hành ABCD, O là giao điểm của AC và BD. các điểm M,N lần lượt là trung điểm của AD, BC. BM,DN cắt AC tại các điểm E,F.Chứng minh: a)AE=EF=FC
b)tứ giác MENF là hình bình hành.
c)để MENF là hình chữ nhật, hình thoi, hình vuông thì ABCD cần thêm điều kiện gì?
Các bạn chỉ cần giải câu c) thôi a,b chỉ là gợi ý và mình cx giải đc rùi.
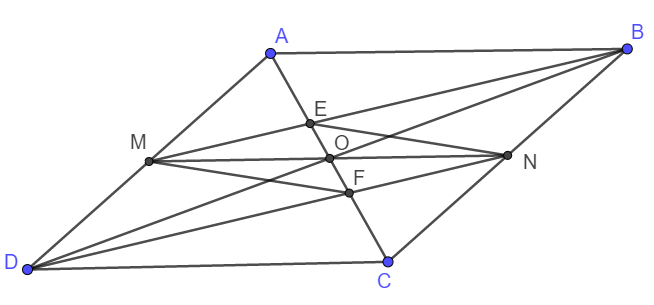
a) Do ABCD là hình bình hành nên AD song song và bằng BC.
Lại có M, N là trung điểm AD, BC nên DM song song và bằng BN. Suy ra DMBN là hình bình hành, hay MB//DN.
Xét tam giác ADF, có:
M là trung điểm AC
ME//DF
\(\Rightarrow\) ME là đường trung bình tam giác ADF.
Vậy AE = EF.
Hoàn toàn tương tự : EF = FC.
Vậy nên AE = EF = FC.
b) DMBN là hình bình hành nên hai đường chéo DB và MN cắt nhau tại trung điểm mỗi đường.
Vậy thì O là trung điểm MN.
Lại có: AO = OC; AE = FC nên AO - AE = OC - FC hay EO = OF.
Xét tứ giác MENF có O là trung điểm hai đường chéo EF và MN nên MENF là hình bình hành.
c)
+) Để hình bình hành MENF là hình chữ nhật thì hai đường chéo MN và EF bằng nhau.
Lại có MN = AB, EF = \(\frac{AC}{3}\). Vậy hình bình hành ABCD phải có đường chéo AC = 2AB thì MENF là hình chữ nhật.
+) Để hình bình hành MENF là hình thoi thì hai đường chéo MN và EF phải vuông góc.
Vậy thì \(EF\perp MN\Rightarrow AC\perp AB\)
Vậy hình bình hành ABCD phải có đường chéo AC vuông góc với cạnh AB thì MENF là hình thoi.
+) Để hình bình hành MENF là hình vuông thì nó vừa là hình chữ nhật, vừa là hình thoi.
Vậy thì hình bình hành ABCD có đường chéo AC vuông góc với AB và AC = 2AB.
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC . Qua M kẻ ME vuông góc với AB tại E ; kẻ MF vuông góc với AC tại F
a) chứng minh AEMF là hình chữ nhật
b) Gọi N là điểm đối xứng với M qua F . Chứng minh AMCN là hình thoi
c)Cho AB=6 ; AC=8 cm . Tính diện tích tứ giác AEMF
Chỉ cần làm cho mình ý b với ý c thôi, có gì mình tick cho
ys c tho
b)có AM=MC (định lý đường trug tuyến tg vuông)
suy ra tg AMC cân tại M. gọi MN cắt AC tại O
mà MO là đg cao( AO vuông góc vs AC)
suy ra MO là trug tuyến (trog tg vuông 1 đg đóng vtro các đg còn lại) suy ra AO=OC
xét tứ giác MANC có: MO=NO; AO=OC suy ra tứ giác này là hình bình hành
có MN vuông góc vsAC suy ra tứ giác này là hình thoj(dấu hiệu nhận biết)
c) có AM=MB (đg trug tyến tg vuông) suy ra tg AMB cân tại M
suy ra BE=AE(1 đg đóng vtro các đg còn lại)
suy ra EA=3cm
có AF=FC( t'c hình thoi)
suy ra AF=4cm
S hình chữ nhật EMFA là;
3 nhân 4 +12(cm2)
cho hình chữ nhật ABCD. Gọi F là trung điểm của CD . Từ F kẻ đường thẳng vuông góc với CD cắt AB tại E
a)cm tú giác FEADlaf hình chữ nhật
b)cm BEDF là hình bình hành
c)Gọi I là giao điểm của EC và BF. Lấy M là điểm đối xứng của I qua BE. cm MEIB là hình thoi
d)Vẽ FH vuông góc với DE tại H. Gọi L là trung điểm của FH và gọi Q là giao điểm của EL và CH. TÍnh FB khi IQ= 6cm
các bạn chỉ cần giải cho mình câu D thôi nhé ! Tại vì mình giải được các câu trên rồi chỉ còn câu d thôi , giúp mình nhé!
(Các bạn chỉ cần làm ý c và d cho mk thôi!)
Cho tam giác ABC có 3 góc nhọn, trực tâm H. Qua B vẽ đường thẳng vuông góc với AB, qua C vẽ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau tại D
a) CM: tứ giác BHCD là hình bình hành
b) Gọi M là trung điểm BC, O là trung điểm AD. CM: M là trung điểm của HD và AH=2OM
c) Tìm điều kiện của tam giác ABC để tứ giác BHCD là hình chữ nhật
d) Gọi G là trọng tâm tam giác ABC. CM: 3 điểm H, G, O thẳng hàng
Cho tam giác ABC vuông tại A,đường trung tuyến A , từ H kẻ HD vuông góc với AB , từ H kẻ HE vuông góc với AC
a) chứng minh ADHE là hình chữ nhật
b) gọi M là trung điểm của HC . Chứng minh tam giác DME là tam giác vuông
c) Cho BC=7,5 ; AB=4,5 . Tính diện tích tam giác ABC
Chỉ cần làm ý b với ý c thôi
Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB
lần lượt cắt các đoạn thẳng AD, BD, AC, BC tại M, N, P, Q.
a/ Chứng minh MN = PQ.
b/ Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
Chứng minh đường thẳng EF đi qua trung điểm của AB và DC.
Chỉ cần ý b thôi nha. Tks
Gọi I là trung điểm của AB.
Giả sử đường thẳng IE cắt CD tại K1
Có: \(\frac{IA}{K_1D}=\frac{EI}{EK_1}=\frac{IB}{K_1C}\) (hệ quả định lý Ta lét)
mà IA = IB (gt) nên K1D = K1C, do đó K1 là trung điểm CD
Giả sử đường thẳng IF cắt CD tại K2
Có: \(\frac{IA}{K_2C}=\frac{FI}{FK_2}=\frac{IB}{K_2D}\) (hệ quả định lý Ta lét)
mà IA = IB (gt) nên K2C = K2D, do đó K2 là trung điểm CD
do IE và IF cùng đi qua trung điểm K của CD nên hai đường thẳng này trùng nhau
Vậy ta có đpcm
Bạn ơi gọi luôn I là trung điểm AB thì sai r
Thực ra bài này cũng có nhiều cách mà em, cách kia cũng không phải là ngộ nhận