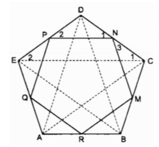
câu 1. ngũ giác ABCDE. M : N: P :Q lần lượt là trung điểm cùa AB: BC ; DE ; AE. I ; K là trung điểm của NQ và MP. cm
a) IK // CD
b) IK = 1/4 CD
câu 2. tìm số cạnh của 1 đa giác đều biết số đo mỗi góc của đa giác đó là 150 độ
câu 3. ngũ giác đều ABCDE. AB giao BE tại I. tứ giác CIED là hình gì? vì sao??
HELP ME, PLEASE![]()