Cho tam giác ABC có AH vuông góc cạnh BC ở H. So sánh các cặp góc sau: BAH và ACB ; HAC và ABC. Biết AB=3cm, AC=4cm, BC=5cm.

Những câu hỏi liên quan
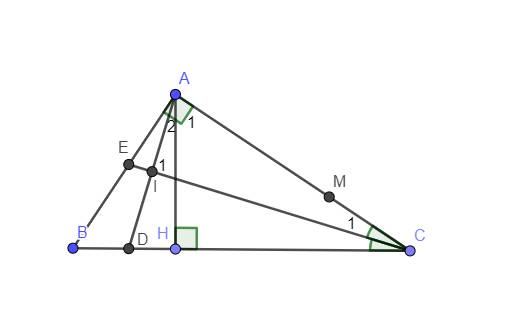
Cho tam giác ABC có góc A = 90 độ. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh góc BAH = góc ACB.
b) Tia phân giác góc BAH và tia phân giác góc ACB cắt nhau tại I. Tính góc AIC
c) Cho AC > AB Trên cạnh AC lấy điểm M sao cho CM= AB. So sánh CM và BH.
`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A.Kẻ AH vuông góc BC (H thuộc B) các tia phân giác của các góc BAH và ACB cắt nhau ở K .Chứng minh AK vuông góc với CK
Bạn tham khảo ở đây:
Câu hỏi của ngô thị gia linh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H , kẻ tia phân giác của góc BAH cắt BC tại D
a) So sánh góc BAH và góc C ; góc CAH và góc B ; góc DAC và góc ADC
b) Kẻ tia phân giác của góc ACB cắt AD tại K . Chứng minh CK vuông góc với AD
HELP ME !!!!!!!!!!
a) \(\widehat{BAH}=\widehat{C}\) (vì cùng phụ với \(\widehat{B}\)) (1)
\(\widehat{CAH}=\widehat{B}\) (vì cùng phụ với \(\widehat{C}\)) (2)
Xét tam giác DAB có: \(\widehat{ADC}=\widehat{DAB}+\widehat{B}\) (vì góc ngoài bằng tổng hai góc trong không kề với nó)
Ta lại có: \(\widehat{DAC}=\widehat{DAH}+\widehat{HAC}\)
Mà \(\widehat{DAB}=\widehat{DAH}\) (tính chất tia phân giác)
\(\widehat{B}=\widehat{HAC}\) (theo (2))
=> \(\widehat{ADC}=\widehat{DAC}\)
b) Theo câu a ta có: \(\widehat{C}=\widehat{HAB}\)
=> \(\widehat{C_1}=\widehat{C_2}=\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ACK có tổng 2 góc A và C là:
\(\widehat{ACK}+\widehat{CAK}=\widehat{C_2}+\widehat{CAK}=\widehat{A_1}+\widehat{CAK}=\widehat{CAB}=90^o\)
=> Góc còn lại bằng 90 độ, tức là \(\widehat{AKC}=180^o-\left(\widehat{ACK}+\widehat{CAK}\right)=180^o-90^o=90^o\)
=> CK vuông góc với AD
Đúng 0
Bình luận (0)
cho tam giác ABC có AB = 3cm ,AC = 4cm
a) So sánh góc B với góc C
b) Hạ AH vuông góc với BC tại H .So sánh góc BAH và góc CAH
a: Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
b: Ta có: \(\widehat{BAH}+\widehat{B}=\widehat{CAH}+\widehat{C}\)
mà \(\widehat{B}>\widehat{C}\)
nên \(\widehat{BAH}< \widehat{CAH}\)
Đúng 1
Bình luận (0)
cho tam giác ABC có AB = 3cm ,AC = 4cm
a) So sánh góc B với góc C
b) Hạ AH vuông góc với BC tại H .So sánh góc BAH và góc CAH
cho tam giác ABC vuông tại A .kẻ AH vuông góc với BC( H thuộc BC).các tia phân giác của các góc BAH và ACB cắt nhau tại K ,chứng minh AK vuông góc với CK
Bạn tham khảo ở đây nhé:
Câu hỏi của ngô thị gia linh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc cạnh BC). Các tia phân giác của các góc C và BAH cắt nhau ở I. Số đo góc AIC là
1. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. Các tia phân giác của góc BAH và góc ACB cắt nhau tại K. CMR: AK vuông góc với CK
1. Cho tam giác ABC nhọn và AB AC có đường cao AH. Kéo dài AH thêm 1 đoạn HD bằng với HA. so sánh tam giác ABH và tam giác BHD; so sánh tam giác ACH và tam giác CDH.2. Trên cùng phía của đường thẳng xy, vẽ hai đường thẳng AH và BK sao cho AH vuông góc xy ở H, BK vuông góc xy ở K và BK AH. so sánh tam gaics AHK và tam giác HKB và so sánh các cặp cạnh và góc tương ứng giữa chúng.Giúp mk vs huhuhu
Đọc tiếp
1. Cho tam giác ABC nhọn và AB < AC có đường cao AH. Kéo dài AH thêm 1 đoạn HD bằng với HA. so sánh tam giác ABH và tam giác BHD; so sánh tam giác ACH và tam giác CDH.
2. Trên cùng phía của đường thẳng xy, vẽ hai đường thẳng AH và BK sao cho AH vuông góc xy ở H, BK vuông góc xy ở K và BK = AH. so sánh tam gaics AHK và tam giác HKB và so sánh các cặp cạnh và góc tương ứng giữa chúng.
Giúp mk vs huhuhu
Cho tam giác ABC có AC>AB, góc ABC > góc ACB. Vẽ AH vuông góc BC ( H thuộc BC). Cho HC>HB.
a. Lấy điểm E trên đoạn thẳng AH. So sánh độ dài đoạn BE và BA
b. So sánh độ dài đoạn CE bà CA
c. So sánh độ dài đoạn EB và EC
a: Ta có: ΔBEH vuông tại H
nên \(\widehat{BEH}< 90^0\)
=>\(\widehat{BEA}>90^0\)
=>BA>BE
b: Ta có: ΔEHC vuông tại H
nên \(\widehat{HEC}< 90^0\)
=>\(\widehat{AEC}>90^0\)
hay CA>CE
c: Xét ΔEBC có HB<HC
mà HB là hình chiếu của EB trên BC
và HC là hình chiếu của EC trên BC
nên EB<EC
Đúng 2
Bình luận (0)













