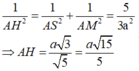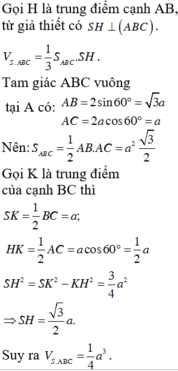10. Cho tam giác ABC có góc A = 60o; Góc C = 50o. Tia phân giác của góc B cắt AC tại D. Tính góc ADB; Góc CDB.

Những câu hỏi liên quan
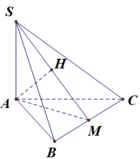
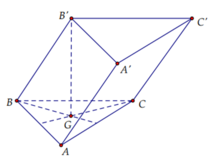
Cho hình lăng trụ tam giác ABC. ABC có BB a, góc giữa đường thẳn BB và mặt phẳng (ABC) bằng
60
o
, tam giác ABC vuông tại C và
B
A
C
^
60
o
. Hình chiếu vuông góc của điểm B lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A.ABC tính theo a bằng
Đọc tiếp
Cho hình lăng trụ tam giác ABC. A'B'C' có BB' = a, góc giữa đường thẳn BB' và mặt phẳng (ABC) bằng 60 o , tam giác ABC vuông tại C và B A C ^ = 60 o . Hình chiếu vuông góc của điểm B' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A'.ABC tính theo a bằng
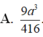
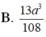
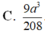
Cho tam giác ABC có các góc ∠ A = 60 o , B = 30 o . So sánh các cạnh của tam giác:
A. AB > AC > BC
B. AB > BC > CA
C. BC > AC > AB
D. CB > AB > AC
Ta có ∠C = 180o - 60o - 30o = 90o
Vì ∠C > ∠A > ∠B ⇒ AB > BC > AC. Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 60o, BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác đó
Áp dụng định lý Sin trong tam giác ABC ta có:
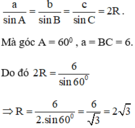
Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.
Đúng 0
Bình luận (0)
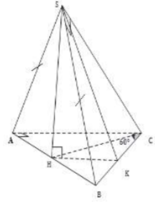
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC 2a , góc ABC
60
o
. Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là: A.
a
3
2
B.
a
3
4
C.
a...
Đọc tiếp
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a , góc ABC = 60 o . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16
Cho tam giác ABC, AB AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.a) CMR: tam giác ABM có 2 góc bằng nhaub) BI là tia phân giác góc ABM, CMR : BI⊥AMc) Cho góc BAC 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?trả lời đúng mình tikk
Đọc tiếp
Cho tam giác ABC, AB < AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.
a) CMR: tam giác ABM có 2 góc bằng nhau
b) BI là tia phân giác góc ABM, CMR : BI⊥AM
c) Cho góc BAC = 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?
trả lời đúng mình tikk
giúp tui ikkkkkk mà sao ko ai trả lời hộ tui vại
Đúng 0
Bình luận (0)
a: Ta có: \(\widehat{ABD}=\widehat{BAM}\)
\(\widehat{DBC}=\widehat{AMB}\)
mà \(\widehat{ABD}=\widehat{DBC}\)
nên \(\widehat{BAM}=\widehat{AMB}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC, AB AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.a) CMR: tam giác ABM có 2 góc bằng nhaub) BI là tia phân giác góc ABM, CMR : BI⊥AMc) Cho góc BAC 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?GIÚP MIK VỚI CẦN GẤP GẤP LẮM Ạ! CẢM ƠN TRƯỚC
Đọc tiếp
Cho tam giác ABC, AB < AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.
a) CMR: tam giác ABM có 2 góc bằng nhau
b) BI là tia phân giác góc ABM, CMR : BI⊥AM
c) Cho góc BAC = 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?
GIÚP MIK VỚI CẦN GẤP GẤP LẮM Ạ! CẢM ƠN TRƯỚC
a: Ta có: \(\widehat{ABD}=\widehat{BAM}\)
\(\widehat{DBC}=\widehat{AMB}\)
mà \(\widehat{ABD}=\widehat{DBC}\)
nên \(\widehat{BAM}=\widehat{AMB}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC, AB AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.a) CMR: tam giác ABM có 2 góc bằng nhaub) BI là tia phân giác góc ABM, CMR : BI⊥AMc) Cho góc BAC 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?trả lời đúng mình tikk
Đọc tiếp
Cho tam giác ABC, AB < AC, BD là tia phân giác góc ABC ( D∈AC). Qua A kẻ đường thẳng song song với BD cắt BC tại M.
a) CMR: tam giác ABM có 2 góc bằng nhau
b) BI là tia phân giác góc ABM, CMR : BI⊥AM
c) Cho góc BAC = 60o , tia phân giác góc ABC cắt BD tại O, tia phân giác góc ngoài tại C cắt đường thẳng BI tại K, tính góc BOC và BKC?
trả lời đúng mình tikk
a: Ta có: \(\widehat{ABD}=\widehat{BAM}\)
\(\widehat{DBC}=\widehat{BMA}\)
mà \(\widehat{ABD}=\widehat{DBC}\)
nên \(\widehat{BAM}=\widehat{BMA}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có ∠A =60o,∠C =50o. Tia phân giác của góc B cắt AC ở D. Tính ∠ADB ,∠CDB
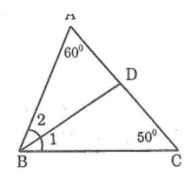
Trong ΔABC ta có:
∠A + ∠B + ∠C = 180o(tổng ba góc trong tam giác)
⇒∠B = 180o - (∠A +∠C )
⇒x = 180o - (60o + 50o) = 70o
(∠B1) =(∠B2 ) = (1/2 )∠B (vì BD là tia phân giác)
⇒ ∠B1 = ∠B2 = 70o : 2 = 35o
Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D
⇒ ∠(ADB) = ∠(B1 ) + ∠C (tính chất góc ngoài tam giác)
Nên ∠(ADB) = 35º + 50º = 85º
+) Do ∠(ADB) + ∠(BDC) = 180o(hai góc kề bù)
⇒∠(BDC) = 180o-∠(ADB) = 180o - 85o = 95o
Đúng 0
Bình luận (0)
Cho tam giác bằng nhau ABC và MNO biết góc A =60o, góc N=80o.Tính các góc còn lại của mỗi tam giác ?
Vì ΔABC=ΔMNO
⇒\(\widehat{A}=\widehat{M};\widehat{B}=\widehat{N};\widehat{C}=\widehat{O}\)
nên \(\widehat{A}+\widehat{B}+\widehat{C}=180\text{°}\)(tổng 3 góc trong 1 tam giác)
\(60\text{°}+80\text{°}+\widehat{C}=180\text{°}\)
\(140\text{°}+\widehat{C}=180\text{°}\)
⇒\(\widehat{C}=40\text{°}\)
⇒\(\widehat{M}=\widehat{A}\left(=60\text{°}\right);\widehat{N}=\widehat{B}\left(=80\text{°}\right);\widehat{C}=\widehat{O}\left(=40\text{°}\right).\)
Đúng 1
Bình luận (0)