Cho △ABC vuông tại A, trung tuyến AM. Gọi E; F là hình chiếu của B và C trên dường thẳng AM. Gọi G là điểm đối xứng của A qua M
a) Chứng minh BE = CF
b) BECF là hình gì
c) Chứng minh BG vuông góc với CG
d) Cho AG = 10cm, EF = 6 cm. Tính BE và CF
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Trung tuyến AM. Gọi I là trung điểm AC. Vẽ Ax // BC, MI cắt Ax tại D
a) chứng minh ADCM là hình thoi
b) Gọi E là trung điểm AM. Chứng minh B,E,D thẳng hàng
Tâm giác vuông ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D. a) Cho BC=6cm. Tính AM b) Chứng minh: MC=AE
a: AM=BC/2=3cm
b: Xét tứ giác AMBE co
D là trung điểm chung của AB và ME
MA=MB
Do đó; AMBE là hình thoi
=>AE=MB=MC
Đúng 0
Bình luận (0)
Cho Tam Giác ABC Vuông Tại A , Đường Trung tuyến AM, gọi D là Trung điễm cũa AB,E là Điễm Đối Xứng M Qua AB
Cho tam giác ABC vuông tại A. AH vuông góc với BC. Trung tuyến AM. Gọi E VÀ F là hình chiếu của H trên AB,AC. Chứng minh EF vuông góc với AM
cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D,E lần lượt là chân đường vuông góc kẻ từ A đến AB, AC. CM: AM vuông góc với DE
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Từ M kẻ vuông góc với AB tại E, vuoing góc với AC tại F. Gọi G là trọng tâm của tam giác ABC CM: ( AG + BC)÷2> BG
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.
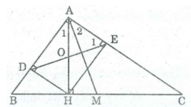
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ∆ ADH và ∆ EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
∠ (ADN) = ∠ (EHD) = 90 0
Suy ra: ∆ ADH = ∆ EHD (c.g.c)
⇒ ∠ A 1 = ∠ (HED)
Lại có: ∠ (HED) + ∠ E 1 = ∠ (HEA) = 90 0
Suy ra: ∠ E 1 + ∠ A 1 = 90 0
∠ A 1 = ∠ A 2 (chứng minh trên) ⇒ ∠ E 1 + ∠ A 2 = 90 0
Gọi I là giao điểm của AM và DE.
Trong ∆ AIE ta có: ∠ (AIE) = 180o – ( ∠ E 1 + ∠ A 2 ) = 180 0 - 90 0 = 90 0
Vậy AM ⊥ DE.
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a. Đường cao AH. Gọi E,F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC. Kẻ trung tuyến AM của tam giác ABC. Chứng minh rằng AM vuông góc với EF
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D. Tam giác ABC có điều kiện gì thì AEBM là hình vuông.
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.a) Cm: tam giác BDK vuông cân tại Db) Cm : (AD/AC)2 2/92/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.a) Cm: BI vuông với IM tại Ib) Cm: AN.AB IC.MK
Đọc tiếp
1/ Cho tam giác ABC vuông tại A có đường phân giác AD và đường trung tuyến BM vuông góc tại E. Gọi H là trung điểm AE. BE cắt AC tại K.
a) Cm: tam giác BDK vuông cân tại D
b) Cm : (AD/AC)2 = 2/9
2/ Cho tam giác ABC vuông cân tại có đường trung tuyến AM. Vẽ MH vuông AB ( H thuộc AB ). Từ A hạ AI vuông CH tại I. Gọi N là giao điểm IC và AM. BI cắt AC tại K.
a) Cm: BI vuông với IM tại I
b) Cm: AN.AB = IC.MK