ABCD là hình thang cân ( AB song song CD ), AC cắt BD tại E. CMR:

a) EA= EB; EC= ED

b) Kẻ đường cao AH, BK

CMR: DH= CK 

ABCD là hình thang cân ( AB song song CD ), AC cắt BD tại E. CMR:

a) EA= EB; EC= ED

b) Kẻ đường cao AH, BK

CMR: DH= CK 

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

a, Xét Δ IDC có

AB // CD => ΔIAB \(\sim\) ΔIDC

=> \(\dfrac{IA}{ID}\) = \(\dfrac{IB}{IC}\) = \(\dfrac{AB}{DC}\)

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\) ; \(\widehat{ODC}=\widehat{OBA}\) ; \(\widehat{AOB}=\widehat{COD}\)

=> ΔOAB \(\sim\) ΔOCD

=> \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)

=> \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{IA}{ID}=\dfrac{IB}{IC}=\dfrac{IA+IB}{ID+IC}=\dfrac{OA+OB}{OC+OD}\)

ok con de

a) Do AE // BC (gt), theo định lí Ta - let, ta có :

            OE/OB   = OA/OC      (1)

Do BF // AD (gt), theo định lí Ta - let, ta có :

            OB/OD   = OA/OC (2)

Từ (1) và (2),suy ra  DECF là hình thang cân.

b)Ta có EF// AB//DC (gt)

AB=5cm;CD=10cm(gt

Đoạn này chả biết nói sao cho dễ hiểu,nhưng mình làm ra thì nó bằng :EF/AB=EF/CD=1/2(chẳng biết đúng hay sai đâu T.T)

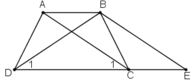
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE     (1)

Theo giả thiết AC = BD     (2)

Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.