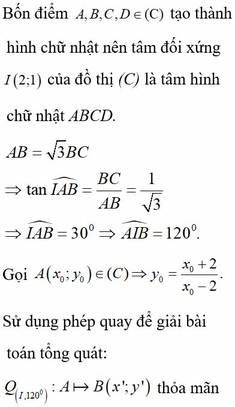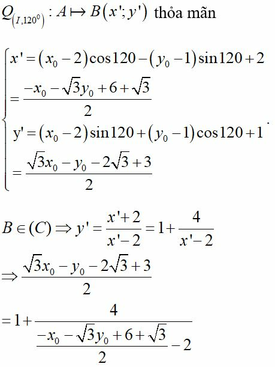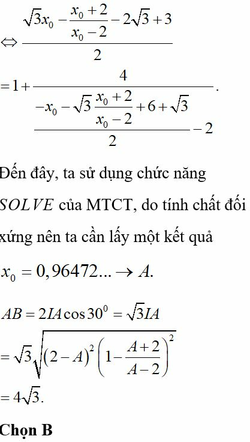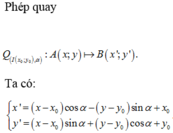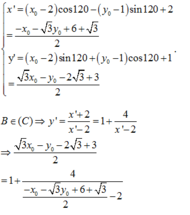Cho hình chữ nhật ABCD có BE = 1/3BC; DG = 2/3 DC ; AE cắt BG tại O. Tính diện tích tam giác AOG biết diện tích tứ giác OECG bằng 270 cm2cm2
(Con làm bài thi ra giấy và nhờ bố mẹ kiểm tra đáp án vào ngày hôm sau)

Những câu hỏi liên quan
Giải bài toán: cho hình chữ nhật ABCD, BE=1/3BC, DG=2/3DC. Tính diện tích tam giác AOG biết diện tích OECG = 270 cm2. Biết E nằm trên đoạn BC, G nằm trên đoạn DC, O là giao điểm của đoạn AE và BG
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 3BC, M(3/2; -3/2) là trung điểm của AD, N là điểm trên cạnh AB thỏa BN = 2AN. Tìm tọa độ các đỉnh của hình chữ nhật ABCD biết phương trình đường AN: x - 3y - 2 = 0 và điểm C có hoành độ dương.
AN chính là đường thẳng AB nên AB: x-2y-2=0.
AD qua M(3/2;-3/2) và vuông góc với AB nên AD: 2x+y-3/2=0. Suy ra A(1;-1/2)
Vì M là trung điểm AD nên D(2;-5/2) suy ra BC=AD=\(\sqrt{5}\), suy ra AB=3BC=3\(\sqrt{5}\)
B(2b+2;b) nên
\(AB=\sqrt{(2b+1)^2+(b+1/2)^2}=\dfrac{\sqrt{5}}{2}|2b+1|=3\sqrt{5}\Rightarrow b=\dfrac{5}{2}\) hoặc \(b=-\dfrac{7}{2}\)
Nếu \(b=\dfrac{5}{2}\) thì B(7;5/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(8;-1/2) (thỏa mãn)
Nếu \(b=-\dfrac{7}{2}\) thì B(-5;-7/2). Do \(\overrightarrow{BC}=\overrightarrow{AD}=(1;-2)\) nên C(-4;-11/2) (loại)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 3BC, M(3/2; -3/2) là trung điểm của AD, N là điểm trên cạnh AB thỏa BN = 2AN. Tìm tọa độ các đỉnh của hình chữ nhật ABCD biết phương trình đường CN: x - 3y - 2 = 0 và điểm C có hoành độ dương.
Đặt BC=a, suy ra AB=3a.
$S_{MNC}=S_{ABCD}-S_{AMN}-S_{BNC}-S_{DMC}=3a^2-\dfrac{a^2}{4}-a^2-\dfrac{3a^2}{4}=a^2$
$CN=a\sqrt{5}$ nên $d(M,CN)=\dfrac{2S_{MNC}}{CN}=\dfrac{2a}{\sqrt{5}}$
Mặt khác $d(M,CN)=\dfrac{4}{\sqrt{10}}$ nên $a=\sqrt{2}$
Suy ra $MC=\dfrac{a\sqrt{37}a}{2}=\dfrac{\sqrt{74}}{2}$
Gọi C(3c+2;c) (3c+2>0) thì
$MC^2=(3c+1/2)^2+(c+3/2)^2=\dfrac{74}{4}\Leftrightarrow (6c+1)^2+(2c+3)^2=74$
$40c^2+24c-64=0$ nên c=1 hoặc c=-8/5(loại) nên C(5;1)
+ Tương tự tìm được N từ việc N thuộc CN, $MN=\dfrac{a\sqrt{5}}{2},CN=a\sqrt{5}$
+ Sau khi tìm được N ta tìm được E từ việc M là trung điểm CE
+ Tọa độ A, B xác định qua hệ thức véc tơ: vecto(EA)=3.vecto(AN); vecto(AN)=2vecto(NB)
+ Tọa độ D xác định từ việc M là trung điểm AD.
Đúng 0
Bình luận (0)
tính diện tích hình bình hành MNPQ vẽ trong hình chữ nhật ABCD . biết AB=28cm ; BC=18cm;AM=CP=1/4 AB;BN=DQ=1/3BC
Ta có: AM = CP = 1/4AB => AM = CP = 1/4 x 28 = 7 (cm) => BM = DP = 28 - 7 = 21 (cm)
BN = DQ = 1/3BC = 1/3 x 18 = 6 (cm) => AQ = NC = 18 - 6 = 12 (cm)
St/giác AMQ = 1/2 xAM x AQ = 1/ 2 x 7 x 12 = 42 (cm2)
St/giác MBN = 1/2 x MB x BN = 21 x 6 x 1/2 = 63 (cm2)
St/giác NPC = 1/2 x NC x CP = 1/2 x 12 x 7 = 42 (cm2)
St/giác QDP = 1/2 x QP x DP = 1/2 x 21 x 6 = 63 (cm2)
SHCN ABCD = 28 x 18 = 504 (cm2) => Shình bình hành MNPQ = 504 - (2 x 42 + 63x 2) = 294 (cm2)
Cho hàm số
y
x
+
2
x
-
2
có đồ thị (C). Xét hình chữ nhật ABCD có
A
B
3
B
C
với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng A. 4 B.
4
3
C.
2
3
D. 3
Đọc tiếp
Cho hàm số y = x + 2 x - 2 có đồ thị (C). Xét hình chữ nhật ABCD có A B = 3 B C với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng
A. 4
B. 4 3
C. 2 3
D. 3
Cho hàm số
y
x
+
2
x
-
2
có đồ thị (C). Xét hình chữ nhật ABCD có
A
B
3
B
C
với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng
Đọc tiếp
Cho hàm số y = x + 2 x - 2 có đồ thị (C). Xét hình chữ nhật ABCD có A B = 3 B C với A, B, C, D là bốn điểm thuộc đồ thị (C). khi đó độ dài AB bằng
![]()
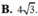
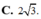
![]()
CHo hình chữ nhật ABCD. Biết 2AB=3BC . Trên BC lấy E . Tia EA cắt DC tại F. CM:\(\frac{1}{4AE^2}+\frac{1}{9AF^2}\)không phụ thuộc vào vị trí của E trên BC
CHo hình chữ nhật ABCD. Biết 2AB=3BC . Trên BC lấy E . Tia EA cắt DC tại F. CM:\(\frac{1}{4AE^2}+\frac{1}{9AF^2}\)không phụ thuộc vào vị trí của E trên BC
Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC=3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình như vậy?
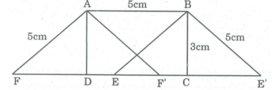
Vẽ cung tròn tâm B bán kính 5cm cắt CD tại 2 điểm E và E'.
Nối BE, từ A kẻ đường thẳng song song với BE cắt CD tại F.
Nối BE', từ A kẻ đường thẳng song song với BE' cắt CD tại F'.
Ta có hình bình hành ABEF và hình bình hành ABE'F' có cạnh AB = 5cm, BE = 5cm, BE' = 5cm có diện tích bằng điện tích hình chữ nhật ABCD.
Có thể vẽ được hai hình như vậy.
Đúng 0
Bình luận (0)