a) Ta có:   d // BC (gt)

 \(\Rightarrow\)B'C' // BC, theo hệ quả của định lí Ta-lét ta có:

     \(\frac{AB'}{AB}=\frac{B'C'}{BC}\)(Trong \(\Delta AB'C'\)và \(\Delta ABC\)) (1)

Và \(\frac{AB'}{AB}=\frac{AD'}{AD}\)(Trong \(\Delta AB'D'\)và \(\Delta ABD\)) (2)

Từ (1), (2) \(\Rightarrow\)\(\frac{B'C'}{BC}=\frac{AD'}{AD}\left(3\right)\)

b) Ta có: AD' = \(\frac{1}{3}\)AD (gt) (4) \(\Leftrightarrow\frac{AD'}{AD}=\frac{1}{3}\left(5\right)\)

Từ (3), (5) \(\Rightarrow\frac{B'C'}{BC}=\frac{1}{3}\Leftrightarrow B'C'=\frac{1}{3}BC\)\(\left(6\right)\)

Tích của cạnh đáy BC và đuuờng cao AD là:

\(S_{ABC}=\frac{1}{2}AD.BC\)

\(\Leftrightarrow\)73,5 \(=\frac{1}{2}AD.BC\)

\(\Leftrightarrow\)\(AD.BC=\)73,5 :\(\frac{1}{2}\)

\(\Leftrightarrow\)\(AD.BC=\)147     \(\left(7\right)\)

Diện tích tam giác AB'C' là:

\(S_{AB'C'}=\frac{1}{2}AD'.B'C'\)

Từ (4), (6) \(\Rightarrow S_{AB'C'}\)=\(\frac{1}{2}.(\frac{1}{3}.AD.\frac{1}{3}BC)\)

                \(\Leftrightarrow S_{AB'C'}=\frac{1}{2}.\frac{1}{3}.\frac{1}{3}.AD.BC\)

Từ (7)  \(\Rightarrow S_{AB'C'}\)\(=\frac{1}{2}.\frac{1}{3}.\frac{1}{3}.147\)

                               \(=\frac{49}{6}\)

Vậy  \(S_{AB'C'}=\frac{49}{6}cm^2\)

Đặt DH = x. Trên tia đối của tia DA em lấy điểm E sao cho DE = DH = x 
=> tam giác BEH cân tại B => ^DBE = ^DBH (1) và BE = BH = 30 
Mặt khác : ^ABD = ^ACD = ^BHD (2) ( góc có cạnh tương ứng vuông góc AC _|_ BH; CD _|_ DH) 
(1) + (2) : ^ABD + ^DBE = ^BHD + ^DBH = 90o => tam giác ABE vuông tại B 
Trong tg ABE vuông tại B đường cao BD nên ta có hệ thức: 
DE.AE = BE² 
<=> DE(AH + DH + DE) = BE² 
<=> x(2x + 14) = 900 
<=> 2x² + 14x - 900 = 0 
Giải ra x = 18 ( loại nghiệm x = - 25) 
=> AD = AH + DH = 14 + 18 = 32

b: góc HID+góc HKD=180 độ

=>HIDK nội tiếp

=>góc HIK=góc HDK

=>góc HIK=góc HCB

=>góc HIK=góc HEF

=>EF//IK

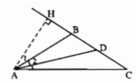
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)

Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º

+) Xét tam giác AHB vuông tại H ta có:

∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)

Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º

+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)

Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên

∠(BAC) = (180º − 112º) : 2 = 34o

+) Do AD là tia phân giác của góc BAC nên

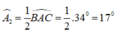
+ Từ đó

∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.

Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º

Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º