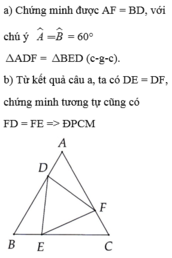
Cho tam giác đều ABC. Lấy các điểm D; E; F theo thứ tự thuộc các cạnh AB; BC; CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều.

Những câu hỏi liên quan
cho tam giác abc đều, lấy các điểm d,e,f theo thứ tự thuộc các cạnh ab,bc,ca sao cho ad=be=cf.Chứng minh tam giác dè là tam giác đều.
Cho tam giác ABC đều. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh:
a) tam giác ADF = tam giác BED.
b) tam giác DEF đều.
Cho tam giác đều ABC. Trên các cạnh AB, BC, CA lấy theo thứ tự các điểm D, E, F sao cho AD=BE=CF. Chứng minh tam giác DEF là tam giác đều
hình chỉ minh họa thôi nhé mk sẽ giải cho
Đúng 0
Bình luận (0)
vì AD=BE=CF nên AD,BE,CF là đường cao là trung trực là tung tuyến phân giác mà 3 đường cao đi qua 1 điểm , điểm này cách đều D,E,F nên tam giác DEF là tam giac đều
Đúng 0
Bình luận (0)
AB=AC=BC
AD=BE=CF
=>BD=EC=AF
Xet ΔADF và ΔBED có
AD=BE
góc A=góc B
AF=BD
=>ΔADF=ΔBED
=>DF=ED
Xét ΔADF và ΔCFE có
AD=CF
góc A=góc C
AF=CE
=>ΔADF=ΔCFE
=>DF=FE=ED
=>ΔDEF đều
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tự thuộc các cạnh AB, BC và CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?
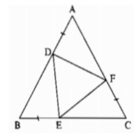
Ta có: AB = AD +DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)
AD = BE = CF ( giả thiết) (5)
Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF
Xét ΔADF và ΔBED, ta có:
AD = BE (gt)
∠A =∠B =60o (vì tam giác ABC đều)
AF = BD (chứng minh trên)
suy ra: ΔADF= ΔBED (c.g.c)
⇒ DF=ED (hai cạnh tương ứng) (6)
Xét ΔADF và ΔCFE, ta có:
AD = CF (gt)
∠A =∠C =60o (vì tam giác ABC đều)
AF = CE (chứng minh trên)
suy ra: ΔADF= ΔCFE (c.g.c)
Nên: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy tam giác DFE đều
Đúng 1
Bình luận (0)
Cho tam giác đều ABC. Lấy các điểm D;E;F theo thứ tự thuộc các cạnhAB;BC;CA sao cho AD=BE=CF. Chứng minh rằng: tam giác DEF là tam giác đều.
AB=AC=BC
AD=BE=CF
=>BD=EC=AF
Xet ΔADF và ΔBED có
AD=BE
góc A=góc B
AF=BD
=>ΔADF=ΔBED
=>DF=ED
Xét ΔADF và ΔCFE có
AD=CF
góc A=góc C
AF=CE
=>ΔADF=ΔCFE
=>DF=FE=ED
=>ΔDEF đều
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Lấy các điểm D; E; F theo thứ tự thuộc các cạnh AB; BC; CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều.
\(\Delta ABC\)đều (gt) nên AB = BC = AC ; góc A = góc B = góc C = 600 mà AD = BE = CF (gt)
=> AB - AD = BC - BE = AC - CF <=> BD = CE = AF
\(\Delta ADF,\Delta BED\)có AD = BE (gt) ; góc DAF = góc EBD = 600 (cmt) ; AF = BD (cmt) nên\(\Delta ADF=\Delta BED\left(c.g.c\right)\)
=> DF = ED (2 cạnh tương ứng) (1)
\(\Delta ADF,\Delta CFE\)có AD = CF (gt) ; góc DAF = góc FCE = 600 (cmt) ; AF = CE (cmt) nên\(\Delta ADF=\Delta CFE\left(c.g.c\right)\)
=> DF = FE (2 cạnh tương ứng) (2).Từ (1) và (2),ta có DF = FE = ED.Vậy\(\Delta DEF\)đều
Đúng 2
Bình luận (0)
. Cho tam giác ABC, Các tia phân giác của các góc B và C cắt nhau tại I Qua I kẻ đường thẳng song song với BC cắt AB tại M và AC tại N. Chứng minh rằng MN = BM + CN
Cho tam giác ABC đều. Trên các cạnh AB, BC, AC lấy 3 điểm theo thứ tự D, E, F sao cho AD=BE=CF
a) CMR tam giác DEF đều
b) Gọi O là giao điểm các dường trung trưc của tam giác ABC. CMR O cũng là giao điểm các đường trung trực của tam giác DEF
Cho tam giác ABC đều . Trên tia đối các tia AB , BC , CA lấy D , E , F sao cho AD = BE = CF . Chứng minh rằng : tam giác DEF đều . cmr tam giác abc và tam giác def có cùng giao điểm của 3 đg trung trực
Xét ΔBDE và ΔAFD có
BE=AD
góc EBD=góc DAF
AF=BD
=>ΔBDE=ΔAFD
=>DE=FD
Xét ΔBDE và ΔCEF có
BE=CF
góc DBE=góc ECF
BD=CE
=>ΔBDE=ΔCEF
=>DE=EF=FD
=>ΔDEF đều
Đúng 0
Bình luận (0)
cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD=BE =CF
CMR: tam giác DEF đều
các bạn giúp mình với. thanks các bạn nhiều

Xét \(\Delta EBD\)và \(\Delta FCE\)có:
EC = DB (Vì \(\hept{\begin{cases}AB=BC\\AD=EB\end{cases}}\))
\(\widehat{EBD}=\widehat{FCE}\)(Cùng là 2 góc ngoài của 1 tam giác đều)
EB = FC (gt)
Suy ra \(\Delta EBD\)\(=\Delta FCE\left(c-g-c\right)\)
\(\Rightarrow DE=EF\)(1)
Chứng minh tương tự: \(\Delta EBD\)\(=\Delta DAF\left(c-g-c\right)\)
\(\Rightarrow DE=FD\)(2)
Từ (1) và (2) suy ra DE = EF = FD
Vậy tam giác DEF đều (đpcm)