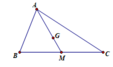
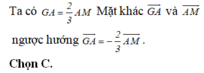Cho tam giác ABC có trọng tâm G và 2 trung tuyến AM=15; BN=12 và tam giác CMN có diện tích là 15\(\sqrt{3}\) . Tính độ dài đoạn thẳng MN.
Những câu hỏi liên quan
Cho tam giác ABC có trung tuyến AM. Gọi H là trực tâm, O là giao điểm các đường trung trực của tam giác ABC. Giao điểm của AM và HO là G. Chứng minh rằng G là trọng tâm của tam giác ABC
1) tam giác ABC có các đường trung tuyến BD và CE bằng nhau . chứng minh rằng tam giác ABC là tam giác cân.
2)cho tam giác ABC cân ở A , AB=34cm , BC =32cm , và 3 trung tuyến AM , BN , CP đồng quy tại trọng tâm G
a) chúng minh AM vuông góc với
b) tính độ dài AM , BN ,CP (làm trong kết quả đến chữ số thập phân thứ 2)
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
Đúng 1
Bình luận (0)
Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là đúng? A.
G
A
→
2
G
M
→
B.
3
M
A
→
+
M...
Đọc tiếp
Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là đúng?
A. G A → = 2 G M →
B. 3 M A → + M B → + M C → = M G →
C. G A → + G B → + 2 G C → = 0 →
D. A M → = - 3 M G →
Do G là trọng tâm tam giác và trung tuyến AM nên AM = 3GM.
Suy ra: A M → = - 3 M G →
Đáp án D
Đúng 0
Bình luận (0)
Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai:
Đọc tiếp
Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai:
Chọn D.
Ta có AM = 3MG. Mặt khác 
và 
ngược hướng 
.
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường trung tuyến AM,gọi G là trọng tâm tam giác,trên tia AM lấy điểm D,sao cho G là trung điểm của AD.Chứng minh:MG=MD và BĐ=CG
Ta có: G là trọng tâm của tam giác
suy ra: MG=1/2AM,suy ra: MG=1/2AG
mà AG=GD suy ra: MG=1/2GD -> MG=MD( điều phải cm)
2. xét tam giác BDM và tam giác CGM
góc GMC=góc DMB (đối đỉnh); GM=MD (cm trên); BM=CM (AM là trung tuyến)
-> tam giác BDM = tam giác CGM(c.g.c)
-> BD=CG (dpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường trung tuyến AM. Điểm G thuộc tia AM là trọng tâm của tam giác ABC. Biết AG=6cm. Độ dài AM là:
A. 8cm
B. 9cm
C. 12cm
D. 14cm
Ta có G là trọng tâm tam giác ABC nên AM = 3/2 AG = 3/2.6 = 9cm. Chọn B
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường trung tuyến AM = 45cm. Điểm G thuộc tia AM là trọng tâm của tam giác ABC. Độ dài AG là:
A. 30cm
B. 45cm
C. 15cm
D. 22,5cm
Do G là trọng tâm tam giác ABC nên AG = 2/3 AM = 2/3.45 = 30cm.
Chọn A
Đúng 0
Bình luận (0)
17 tháng 9 2017 lúc 20:36
Cho tam giác ABC, trung tuyến AM, G là trọng tâm tam giác ABC. Gọi D và N lần lượt là trọng tâm của tam giác AMB và tam giác AMC. Chứng minh rằng 3 điểm D;G;N thẳng hàng?
ta gọi AH,AK là 2 đường trung tuyến của tam giác ABM và AMC
ta có D,G,N lần lượt là trọng tâm tam giác ABM,ABC,AM
=> \(\frac{AD}{AH}=\frac{AG}{AM}=\frac{AN}{AK}=\frac{2}{3}\) (tính chất trọng tâm)
=> DG//BC(đingj lí ta lét) và GN//BC(định lí ta lét )
=> D,G,N thẳng hàng(ĐPCM)
Đúng 0
Bình luận (0)
bạn ơi xem lại đề đi sao M lại là trọng tâm của tam giác AMB?
Đúng 0
Bình luận (0)
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó
G
A
→
A.
2
G
M
→
B.
2
3
G
M
→
C.
-...
Đọc tiếp
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
A. 2 G M →
B. 2 3 G M →
C. - 2 3 A M →
D. 1 2 A M →
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó
G
A
→
Đọc tiếp
Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó G A → =
Chọn C.
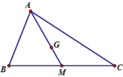
Ta có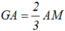 
.Mặt khác 
và 
ngược hướng =>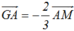
.
Đúng 0
Bình luận (0)