cho tam giác abc. M, N lần lượt trên AB và AC sao cho AM = 2/3 MB; AN =2/3 NC.
a. So ssánh diên tích tam giác MBC và NBC
b. So sánh diện tích MNBCvà diện tích tam giác ABC
1. Cho tam giác ABC. Lấy điểm M; N trên AB và AC sao cho AM = MB; AN = NC. Tính diện tích tam giác AMN. Biết diện tích tam giác ABC bằng 180cm2
2. Cho tam giác ABC. Lấy điểm M; N trên AB và AC sao cho AM = MB; AN = 2.NA Tính diện tích tam giác AMN. Biết diện tích tam giác ABC bằng 300cm2
3. Cho tam giác ABC. Lấy điểm M; N trên AB và AC sao cho AM = MB; AN = NC. Tính diện tích tam giác AMN. Biết diện tích tam giác ABC bằng 120cm2
Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90
cho tam giác abc trên ab lấy điểm m sao cho am = 2 lần mb trên ac lấy điểm n sao cho an = 2 lần nc nối m với n ta được tam giác amn 120 cm mét vuông tính diện tích abc
Xét ΔAMN và ΔABC có AM/AB=AN/AC
nên MN//BC
=>ΔAMN đồng dạng với ΔABC
=>S AMN/S ABC=(AM/AB)^2=4/9
=>S ABC=120:4/9=270cm2
Cho tam giác ABC, M và N lần lượt thuộc AB và AC, biết MN//BC , AM=2, MB = 3, AN = 1,5. Tính AC bằng bao nhiêu?
(Bạn tự vẽ hình nha)
Vì \(MN//BC\) \(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
\(\Leftrightarrow\dfrac{AM}{AM+MB}=\dfrac{AN}{AC}\)
\(\Leftrightarrow\dfrac{2}{2+3}=\dfrac{1,5}{AC}\Rightarrow AC=\dfrac{15}{4}\)
Cho tam giác ABC . Trên cạnh AB lấy điểm M sao cho AM = 2 lần MB , trên cạnh AC lấy điểm N sao cho AN= NC . Biết S tam giác ABC = 180 cm2 . Tính S tam giác AMN . Và S tam giác AMC .
Cho tam giác ABC đều. Các điểm M, N lần lượt di chuyển trên các cạnh AB, AC sao cho AM/MB+AN/NC=1. Tìm vị trí của M, N để diện tích tam giác AMN lớn nhất.
G/s: Tam giác đều ABC có cạnh bằng a
Đặt AM=x, AN =y, x, y dương và bé hơn a
=> MB=a-x, NC=a-y
Theo bài ra ta có:
\(\frac{x}{a-x}+\frac{y}{a-y}=1\)
\(\Leftrightarrow-\frac{x}{a-x}-\frac{y}{a-y}=-1\)
\(\Leftrightarrow1-\frac{a}{a-x}+1-\frac{a}{a-y}=-1\)
\(\Leftrightarrow\frac{a}{a-x}+\frac{a}{a-y}=3\)
\(\Leftrightarrow\frac{3}{a}=\frac{1}{a-x}+\frac{1}{a-y}\ge\frac{\left(1+1\right)^2}{a-x+a-y}=\frac{4}{2a-\left(x+y\right)}\)
\(\Leftrightarrow x+y\le\frac{2a}{3}\)
Diện tích tam giác AMN:
\(S_{\Delta AMN}=\frac{1}{2}AM.AN.\sin\widehat{MAN}=\frac{1}{2}.xy.\frac{\sqrt{3}}{2}\)
\(=\frac{\sqrt{3}}{4}.xy\le\frac{\sqrt{3}}{4}\frac{\left(x+y\right)^2}{4}\le\frac{\sqrt{3}}{16}\frac{4a^2}{9}=\frac{\sqrt{3}a^2}{36}\)
Dấu "=" xảy ra khi và chỉ khi: \(x=y=\frac{a}{3}\)
Vậy AM=1/3AB, AN=1/3AC thì diện tích tam giác AMN lớn nhất bằng \(\frac{\sqrt{3}a^2}{36}\)
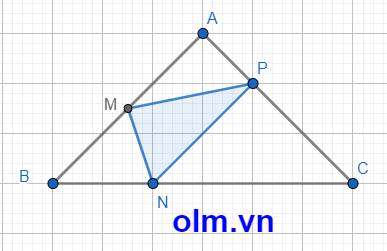
SAMP = \(\dfrac{1}{2}\)SABP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
AP = AC - PC = AC - \(\dfrac{2}{3}\) AC = \(\dfrac{1}{3}\)AC
SAPB = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và AP = \(\dfrac{1}{3}\) AC)
⇒ SAMP = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
SBMN = \(\dfrac{1}{2}\)SABN (vì hai tam giác có chung chiều cao hạ từ đỉnh N xuống đáy AB và BM = \(\dfrac{1}{2}\) AB)
SABN = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BN = \(\dfrac{1}{3}\)BC)
SBMN = \(\dfrac{1}{2}\times\) \(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC
SCNP = \(\dfrac{2}{3}\)SBCP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{2}{3}\) BC)
SBCP = \(\dfrac{2}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và PC = \(\dfrac{2}{3}\)CA)
SCNP = \(\dfrac{2}{3}\times\dfrac{2}{3}\) = \(\dfrac{4}{9}\)\(\times\)36 = 16 (cm2)
Diện tích tam giác MNP là:
36 - (6+6+16) = 8 (cm2)
Đáp số: 8 cm2
Cho tam giác ABC có diện tích 135 cm2. Trên các cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho AM MB, BN NC và CP 2 3 CA. Tính diện tích tam giác MNP
Cho tam giác ABC có diện tích 48 cm2. Trên các cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho AM MB, BN NC và CP 2 3 CA. Tính diện tích tam giác MNP