Biết AD frac{1}{3}AB; AIIMChứng minh : MBMC A B C D I M
Đọc tiếp
Biết AD = \(\frac{1}{3}\)AB; AI=IM
Chứng minh : MB=MC
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A , phân giác trong AD và phân giác ngoài AE.Cho biết AB<AC.CMR
a, \(\frac{1}{AB}+\frac{1}{AC}=\frac{\sqrt{2}}{AD}\)
b,\(\frac{1}{AB}-\frac{1}{AC}=\frac{\sqrt{2}}{AE}\)
a/ \(S_{ABD}=\frac{1}{2}AB.AD.sin\widehat{BAD}=AB.AD.\frac{\sqrt{2}}{4}\)
\(S_{ACD}=\frac{1}{2}AC.AD.sin\widehat{CAD}=AC.AD.\frac{\sqrt{2}}{4}\)
\(S_{ABC}=\frac{1}{2}AB.AC\)
Suy ra : \(S_{ABC}=S_{ABD}+S_{ACD}\Leftrightarrow\frac{1}{2}AB.AC=\frac{\sqrt{2}}{4}AD.\left(AB+AC\right)\Rightarrow\frac{1}{AB}+\frac{1}{AC}=\frac{\sqrt{2}}{AD}\)
b/ Tương tự
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\), phân giác AD biết \(\frac{1}{AD}=\frac{1}{AB}+\frac{1}{AC}.\)Tĩnh số đo góc BAC.
Tam giác ABC cậu tự vẽ nhó =(
Kẻ DE//AB(E∈AC)DE//AB(E∈AC)
Vì AD là phân giác của ˆBACBAC^
⇒ˆBAD=ˆCAD⇒BAD^=CAD^
Vì DE//ABDE//AB
⇒ˆADE=ˆBAD⇒ADE^=BAD^
⇒ˆADE=ˆCAD⇒ADE^=CAD^
⇒ΔDAE⇒ΔDAEcân tại EE
⇒DE=AE⇒DE=AE
Đặt DE=AE=aDE=AE=a
Vì DE//ABDE//ABnên theo hệ quả của định lí Talet ,ta có :
DEAB=CEACDEAB=CEAC
⇒aAB=AC−AEAC⇒aAB=AC−AEAC
⇒aAB=1−aAC⇒aAB=1−aAC
⇒aAB+aAC=1⇒aAB+aAC=1
⇒1AB+1AC=1a⇒1AB+1AC=1a
Mà 1AB+1AC=1AD1AB+1AC=1AD
⇒1a=1AD⇒1a=1AD
⇒a=AD⇒a=AD
⇒DE=AE=AD⇒DE=AE=AD
⇒ΔDAE⇒ΔDAEđều
⇒ˆCAD=60o⇒CAD^=60o
⇒ˆBAC=2ˆCAD=2.60o=120o⇒BAC^=2CAD^=2.60o=120o
Vậy ˆBAC=120o
1.cho tam giác ABC vuong tại A có AD là duong phan giác góc A( D thuoc BC) biết AB= c,AC=b và AD=d
cm\(\frac{\sqrt{2}}{d}=\frac{1}{b}+\frac{1}{c}\)
2.Cho a,b,c là 3 số nguyên dương thỏa mãn a+b+c+ab+bc+ca=6abc
cmr:\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)>=3
cho hình thang ABCD(BC//AD,và AB và CD thuộc M).biết tỉ số \(\frac{MA}{MA}=\frac{5}{3}\)và AD=2,5dcm.Tính BC
Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho:
\(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\)
a) Xác định E. F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP)
b) Chứng minh rằng các đường thẳng NE, PE và CD cùng đi qua một điểm
Tham khảo:
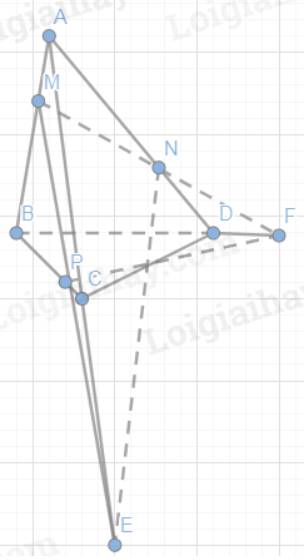
a) Tam giác ABC có: MP cắt AC tại E
Mà MP thuộc (MNP)
Nên E là giao điểm của AC và (MNP)
Tam giác ABD có: MN cắt BD tại F
Mà MN thuộc (MNP)
Nên F là giao điểm của BD và (MNP)
b) Ta có: P thuộc BC
F thuộc BD
Suy ra PF thuộc (BCD)
Do đó PF và CD cùng thuộc (BCD)
Nên PF và CD cắt nhau tại một điểm (1)
Ta có: N thuộc AD
E thuộc AC
Suy ra NE thuộc (ACD)
Do đó NE và CD cắt nhau tại một điểm (2)
Từ (1) và (2) suy ra: NE, PE, CD cùng đi qua một điểm
Đúng 0
Bình luận (0)
Cho tam giác ABC, phân giác AD.CMR: a) Nếu widehat{A} ^{120^o} thì frac{1}{AD}frac{1}{AB}+frac{1}{AC}.b) Nếu widehat{B}90^othì frac{sqrt{2}}{AB}frac{1}{AB}+frac{1}{AC}.c) Nếu widehat{C}60^othì frac{sqrt{3}}{AD}frac{1}{AB}+frac{1}{AC}.
Đọc tiếp
Cho tam giác ABC, phân giác AD.
CMR: a) Nếu \(\widehat{A}\)= \(^{120^o}\) thì \(\frac{1}{AD}=\frac{1}{AB}+\frac{1}{AC}\).
b) Nếu \(\widehat{B}=90^o\)thì \(\frac{\sqrt{2}}{AB}=\frac{1}{AB}+\frac{1}{AC}\).
c) Nếu \(\widehat{C}=60^o\)thì \(\frac{\sqrt{3}}{AD}=\frac{1}{AB}+\frac{1}{AC}\).
cho tam giác ABC vuông tại A trung tuyến AD ,trọng tâm G . a)cho biết \(\frac{AB}{AC}=\frac{3}{4}\)và AD=5cm . Tính diện tích của tam giác ABC
b)qua G kẻ đường thẳng cắt AB, AC lần lượt tại M,N .CMR \(\frac{AB}{AM}+\frac{AC}{AN}=3\)
3 tháng 3 2020 lúc 9:00
Cho tam giác ABC có 3 đường phân giác AD, BE, CF. Chứng minh rằng: \(\frac{1}{AD}+\frac{1}{BE}+\frac{1}{CF}>\frac{1}{AB}+\frac{1}{BC}+\frac{1}{CA}\)
Bài này bọn e đã từng làm rồi, có trong đề thi HSG Toán lớp 8 tỉnh Bắc Giang , anh tham khảo nhé :
Đặt \(BC=a,CA=b,AB=c.\) Độ dài các đường phân giác trong của tam giác kẻ từ các đỉnh A,B,C lần lượt là \(l_a,l_b,l_c\).
Cho hình thang vuông ABCD (\(\widehat{A}=\widehat{D}\)=90) có hai đường chéo AC và BD vuông góc với nhau tại O
a) Biết AB=4cm, CD=9CM.Tính AD?
b) Cm: \(\frac{1}{AO^2}=\frac{1}{AB^2}+\frac{1}{AD^2}\)
Cho hình vuông ABCD cạnh 7,8 . Trên cạnh AB có AM bằng \(\frac{2}{3}\)AB , trên cạnh AD có AN bằng \(\frac{1}{3}\) AD
CHO MÌNH BIẾT CÁCH LÀM NHÉ
AI NHANH NHẤT SẼ ĐƯỢC TICK ĐÚNG