Cho hình bên, trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK; AH = BK

Những câu hỏi liên quan
Cho hình 56.
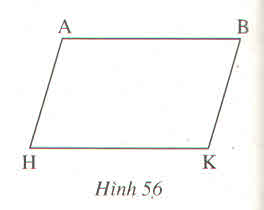
Trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK, AH = BK ?
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
Đúng 0
Bình luận (0)
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................
Đúng 0
Bình luận (0)
Vẽ đoạn thẳng AK.
* Xét △AKB và △KAH có:
góc AKB = góc HAK ( so le trong)
AH là cạnh chung
góc BAK = góc AKH ( so le trong)
Do đó: △AKB=△KAH (g.c.g)
=> AB=HK ( hai cạnh tương ứng)
=> AH=BK ( hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD( AB//CD,AB CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD△BKC
b) ABHK
c) KC(DC-AB):2
Đọc tiếp
Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD=△BKC
b) AB=HK
c) KC=(DC-AB):2

Cho hình thang cân ABCD( AB//CD,AB CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD△BKC
b) ABHK
c) KC(DC-AB):2
Đọc tiếp
Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD=△BKC
b) AB=HK
c) KC=(DC-AB):2

Cho hình thang cân ABCD( AB//CD,AB CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD△BKC
b) ABHK
c) KC(DC-AB):2
Đọc tiếp
Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng
a)△AHD=△BKC
b) AB=HK
c) KC=(DC-AB):2

Cho hình thang cân ABCD( AB//CD,AB CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng:a. Chứng minh ΔAHD ΔBKC . ( Hình 4)b) Chứng minh AB HK c) Chỉ ra: KC (AB - BD):2
Đọc tiếp
Cho hình thang cân ABCD( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng:
a. Chứng minh ΔAHD = ΔBKC . ( Hình 4)
b) Chứng minh AB = HK
c) Chỉ ra: KC= (AB - BD):2
a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
b: Xét tứ giác ABKH có
AB//KH
AH//BK
=>ABKH là hình bình hành
=>AB=KH
Đúng 2
Bình luận (1)
Cho hình thang ABCD (AB // CD) các tia phân giác góc ngoài đỉnh A và
D cắt nhau tại H. Tia phân giác góc ngoài đỉnh B và C cắt nhau ở K. Chứng
minh rằng
a. AH DH ; BK CK
b. HK // DC
c. Tính độ dài HK biết AB = a
CD = b ; AD = c ; BC = d
a. Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠(M') = ∠A2(sole trong)
∠A1= ∠A2(gt)
⇒ ∠(M') = ∠A1nên ΔADM' cân tại D
* DM là phân giác của ∠(ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠(N') = ∠B1nên ΔBCN' cân tại C.
* CN là phân giác của ∠(BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ PN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN = M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
b)MN=AB+M′N′/2 (tính chất đường trung bình của hình thang)
⇒MN=AB+M′D+CD+CN′/2(1)
Mà M′D=AD,CN′=BC. Thay vào (1)
MN=AB+AD+CD+BC/2=a+d+c+b/2
Cho hình thang ABCD (AB//CD) các tia phân giác góc ngoài tại đỉnh A và đỉnh D cắt nhau tại A tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại R Chứng minh rằng: a. AH vg góc DH, BK vg góc CK b. HK//DC c. Tính độ dài HK biết AB=a, CD=b, AD=c, BC=d
Xem chi tiết
Bài 1: Cho hình thang cân ABCD ( AB là đáy bé). Vẽ AH và BK cùng vuông góc với DC (HK thuộc DC). Chứng minh rằng: DH = CK
Giải chi tiết giúp mình nhé. Thanks nhìu !
hình tự vẽ nhé! :)
có HT ABCD cân
=>AD=BC và góc D=góc C
xét tg AHD và tg BKC có:
g. AHD=g.BKC=90*
AD=BC
g.D=g.C
=>tg AHD=tg BKC( cạnh huyền-gn)
=>DH=CK=>dpcm :)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Gọi O là trung điểm của AB, E là điểm đối xứng vs H qua O,F là trung điểm của AH. Kẻ HK vuông góc AC tại K.
a) Chứng minh AHBE là hình chữ nhật
b) Chứng minh 3 điểm E,F,C thẳng hàng
c)Chứng minh hệ thức AH.HC=AC.HK
d)Gọi I là trung điểm của đoạn thẳng HK. Chứng minh rằng AI vuông góc với BK




















