Chọn C.

Đáp án B

Diện tích đáy ABCD là S_ABCD = AB. BC = a.2a = 2a².

Thể tích khối chóp S.ABCD là:

  V = 1 3 . S A . S A B C D = 1 3 . 2 a . 2 a 2 = 4 a 3 3

Đáp án A

Ta có: 

V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3

Đáp án C

 Ta có: S C → . B D → = S A → + A C → . B D → = S A → . B D → + A C → . B D → = A C → . B D →

          = A C . B D . cos D O C ^ = A C 2 . O D 2 + O C 2 − D C 2 2 O D . O C  

          = A C 2 . O D 2 + O C 2 − D C 2 2 O C 2 = 2 2 O C 2 − D C 2

            = 2 5 a 2 2 − a 2 = 3 a 2  

Do đó: cos S C → , B D → = S C → . B D → S C . B D = 3 a 2 3 a . a 5 = 1 5  

Vậy cos S C , B D = cos S C → , B D → = 1 5

Chọn B

Đáp án D

Diện tích hình chữ nhật ABCD là S = 2a², chiều cao SA =a.

Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3

Đáp án B

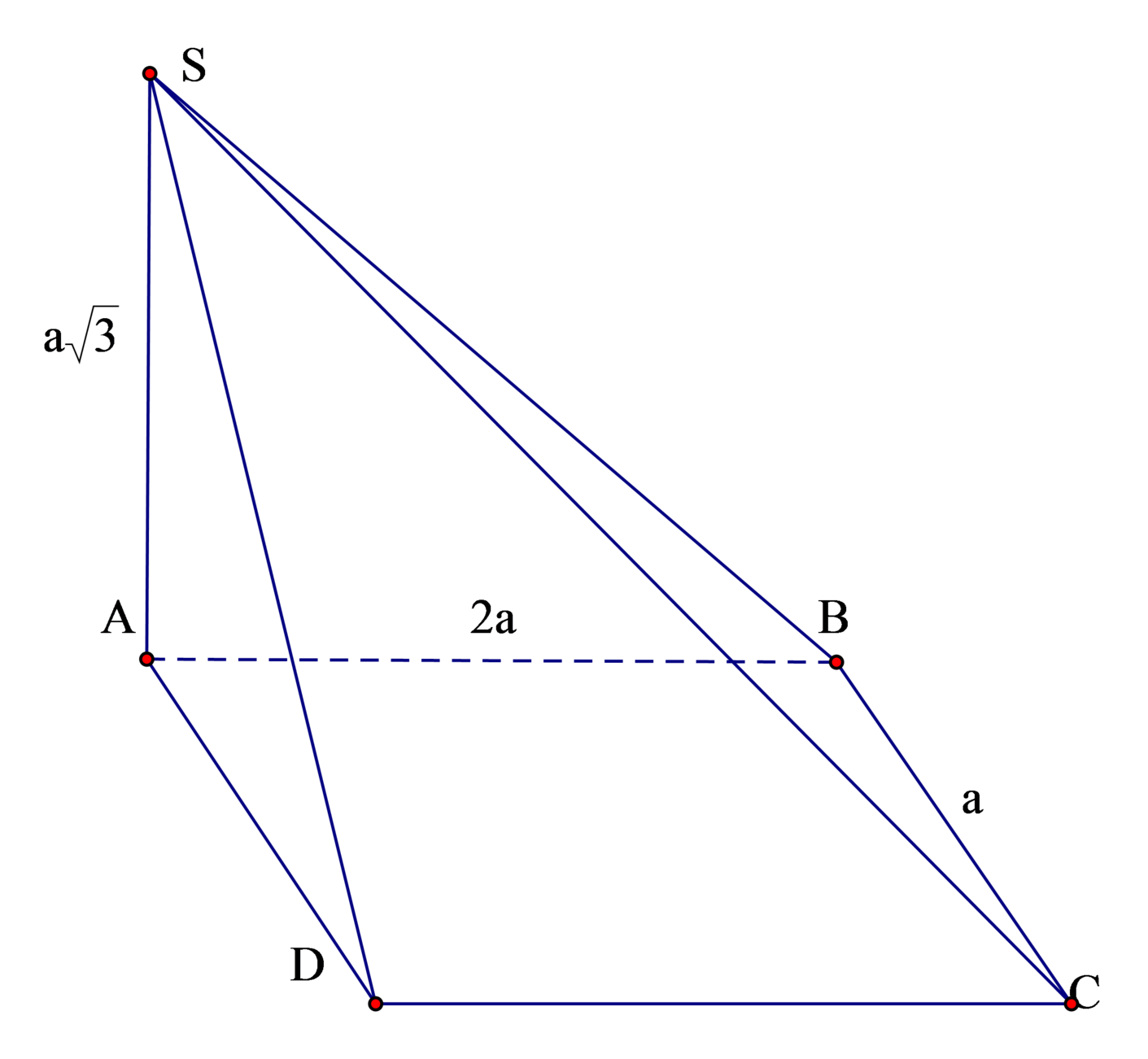
Do S A ⊥ A B C D

⇒ V S A B C D = 1 3 S A . d t A B C D = 1 3 S A . A B . B C = 1 3 a 3 .2 a . a = 2 a 3 3 3