Cho hình thang vuông ABCD (cạnh bên AB và DC): AB = 12cm; AD = 24cm;
BC= AD.
a. Tính diện tích hình thang ABCD.
b. Kéo dài cạnh bên AB và DC chúng gặp nhau tại K. Tính độ dài đoạn KB.
(gợi ý câu b: Nối B với D)
hứa tick ạ
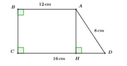
Cho hình thang vuông ABCD có hai đáy AB = 12cm, DC = 16cm, cạnh xiên AD = 8cm. Tính các góc và cạnh góc vuông của hình thang.
A. B C = 3 3 c m , A ^ = 120 0 , D ^ = 60 0
B. B C = 4 3 c m , A ^ = 120 0 , D ^ = 60 0
C. B C = 3 3 c m , A ^ = 135 0 , D ^ = 45 0
D. B C = 4 3 c m , A ^ = 135 0 , D ^ = 45 0
![]()
Có hình thang vuông ABCD cạnh xiên AD
![]()
Dễ thấy ABCH là hình chữ nhật (có 3 góc vuông) => HC = AB = 12cm
HD = DC – HC = 16 – 12 = 4 (cm)
Áp dụng định lý Pytago cho AHD vuông tại H ta có:
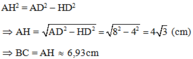
Xét AHD vuông tại H ta có:
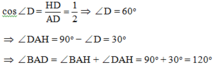
Đáp án cần chọn là: B
CHO HÌNH THANG VUÔNG ABCD ( GÓC A = GÓC D=90 ĐỘ),ĐƯỜNG CHÉO BD VUÔNG GÓC VỚI CẠNH BÊN BC. BIẾT AD=12CM,DC=25CM. TÍNH ĐỘ DÀI AB,BC VÀ ĐƯỜNG CHÉO DB.
Cho hình thang vuông ABCD có hai đáy AB= 12cm, DC= 16cm, cạnh xiên AD= 8cm. Tính các góc và cạnh góc vuông của hình thang.
Cho hình thang vuông ABCD có góc A=góc D=90 độ. Đường chéo BD vuong góc với cạnh bên BC. Biết AD=12cm, DC=25cm. Tính độ dài các cạnh AB, BC và đường chéo BD.
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~
Cho hình thang cân ABCD có AB // DC và AB<DC, đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH
a) Chứng minh △BDC đồng dạng với △HBC
b) Cho BC= 15cm, DC= 25cm. Tính HC và HD
c) Tính diện tích hình thang ABCD
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng vói ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Cho hình thang cân ABCD có AB//DC và AB<DC, đường chéo BD vuông góc với cạnh bên C.Về đường cao BH. a Chứng minh ABDC đồng dạng A HBC b Cho BC=15cm DC=25. Tính HC và HD • Tính diện tích hình thang ABCD.
a:Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
cho hình thang vuông ABCD.Đáy lớn DC bằng 12cm,đáy bé AB=2/3DC.Đường cao AD bằng 6cm.
a) Tính diện tích hình thang ABCD.
b) Kéo dai các cạnh bên DA và CB cắt nhau tại K.Tính độ dài AK?
giúp mik với ạ, vẽ hình và giải chi tiết cho mik nha!
1)Cho đoạn thẳng AB= 13cm. Vẽ nửa đường tròn tâm O , đường kính AB . Từ điểm C trên nửa đường tròn, kẻ CD vuông góc AB . Tính BH và HC
2) CHo hình thang vuông ABCD (góc A = góc D =90 độ ) , đường chéo BD vuông góc với cạnh bên BC. Biết AD=12cm , DC = 25cm .Tính độ dài các cạnh AB và đường chéo DB
cho hình thang vuông ABCD, AD = 6cm; DC = 12cm; AB = 2/3 DC.
A, Tính Diện tích hình thang ABCD
B, Kéo dài các cạnh AD và BC, chúng gặp nhau tại K. Tính độ dài cạnh KA
a: AB=2/3*12=8cm
S=1/2(12+8)*6=60cm2
b: Xét ΔKDC có AB//DC
nên AB/DC=KA/KD
=>KA/(KA+6)=2/3
=>2KA+12=3KA
=>-KA=-12
=>KA=12cm
cho hình thang ABCD ( như hình vẽ bên ) biết AB = 6cm, AD = 12cm , BC = 2/3 AD
a)tính SABCD
b)kéo dài các cạnh bên AB và DC chúng gặp nhau tại K ( như hình vẽ )tính độ dài đoạn KB