Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm: AD và CD nếu BD = 5cm; AC = 8cm
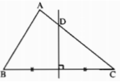
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm :
a) AD và CD nếu BD = 5cm, AC = 8cm
b) AC nếu BD = 11,4cm; AD = 3,2 cm
a: Vì D nằm trên đường trung trực của BC nên DB=DC=5cm
=>AD=8-5=3(cm)
b: D nằm trên đường trung trực của BC nên DB=DC=11,4(cm)
AC=AD+CD=3,2+11,4=14,6(cm)
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Hãy tìm: AC nếu BD = 11,4cm; AD = 3,2cm
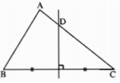
Ta có AC = AD + DC = AD + BD = 3,2 + 11,4 = 14,6 (cm).
Đường trung trực của cạnh BC trong tam giác ABC cắt cạnh AC tại D. Cho AC = 10cm, BD = 4cm. Khi đó AD là:
A. 6cm
B. 4cm
C. 3cm
D. 5cm
Ta chứng minh được ΔBDM = ΔCDM nên BD = DC = 4cm. Khi đó AD = 6cm Chọn A
cho tam giác ABC vuông tại A coa AB=AC=5cm đường phân giác BD(D thuộc AC ) . kẻ DH vuông góc với BC tại H .a) tính độ dài cạnh BC b) chứng minh tam giác ABD = tam giác HBD và BD là đường trung trực của AH c) trên cạnh AB lấy E sao cho AC=AD . đường vuông góc với BD kẻ từ E cắt BC ở G . chứng minh GH=HC
Cho tam giác ABC đều có cạnh là 60cm. lấy điểm D trên BC sao cho BD =20cm. đường trung trực của AD cắt AB tại E, cắt AC tại F. Tính độ dài các cạnh của tam giác ABC
gọi O là giao điểm ba đường trung trực của ba cạnh tam giác ABC. Tia AO cắt BC tại D. Trên cạnh AB lấy điêm E sao cho DE =DB; tên cạnh AC lấy điểm F sao cho Df=Dc
CMRa) Hk song song AB.
b) AC*BD=AB*CD+AD*BC
Cho tam giác ABC vuông tại A, có góc ABC = 60*. Trên tia BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại E, cắt tia BA tại F.
a) Tính số đo góc ACB và so sánh độ dài các cạnh của tam giác ABC.
b) Chứng minh: BE là đường trung trực của đoạn thẳng AD và BE là tia phân giác của góc ABC.
c) Chúng minh: AD // FC.
d) Chứng minh: AC = 3DE.
Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??
cho tam giác ABC đều có cạnh là 60 cm. trên BC lấy điểm D sao cho BD=20cm. Trung trực của AD cắt AB tại E, cắt AC tại F.tính độ dài các cạnh của tam giác ABC