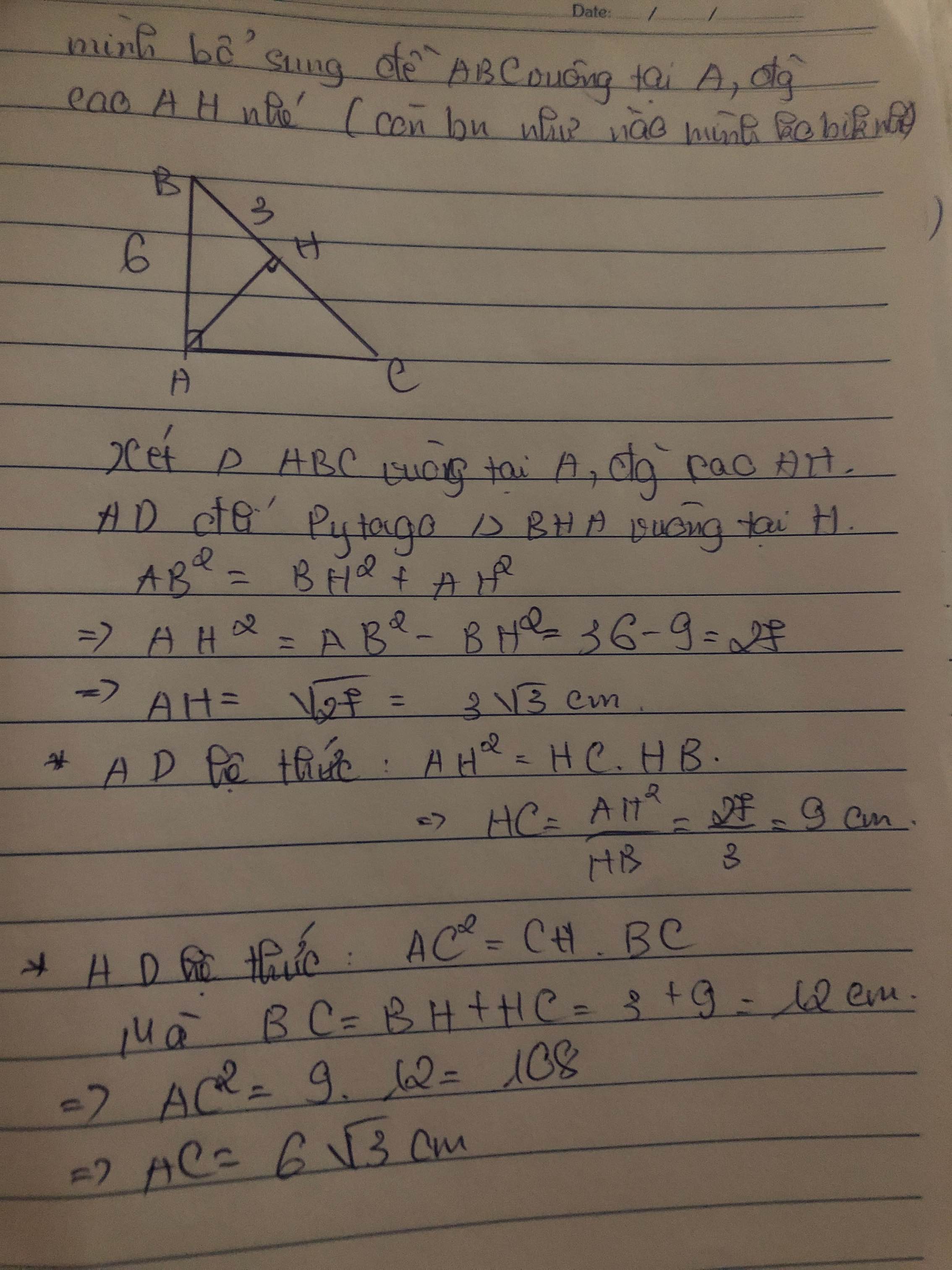Cho ABC có AB = 3cm; AC = 4cm; BC = 5cm
a. Chứng minh tam giác ABC vuông tại A.
b. Vẽ phân giác BD (D ϵ AC)từ D vẽ DE vuông góc với BC (E ϵ BC). Chứng minh DA = DE.
c. ED cắt AB tại F. Chứng minh ΔADF = ΔEDC rồi suy ra DF > DE.

Những câu hỏi liên quan
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A , có AB = √3cm , BC = 2√3cm , tính tỉ số lượng giác của góc B
\(\sin\widehat{B}=\sin60^0=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{B}=\dfrac{1}{2}\)
\(\tan\widehat{B}=\sqrt{3}\)
\(\cot\widehat{B}=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (1)
Cho tam giác ABC có AB=3cm, BC=5cm, ABC^=120 độ. Tính độ dài AC
Vì \(\widehat{ABC}\) là góc tù nên AC>BC>AB(1)
Xét \(\widehat{ABC}\) có:
BC+AB>AC (bất đẳng thức tam giác)(2)
Từ (1)(2)=> BC<AC<BC+AB
5<AC<8
=> AC=6cm hoặc AC=7cm
Đúng 1
Bình luận (1)
Theo định lí cos
\(AC^2=AB^2+BC^2-2cosABC.AB.BC=49\Rightarrow AC=7cm\)
Đúng 0
Bình luận (0)
Cho ∆ABC có AC = 3cm, BC = 5cm, góc BCA = 60°. Tính AB
\(\cos BCA=\dfrac{BC^2+AC^2-AB^2}{2\cdot AC\cdot BC}\)
\(\Leftrightarrow5^2+3^2-AB^2=2\cdot3\cdot5\cdot\dfrac{1}{2}=15\)
hay \(AB=\sqrt{19}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB\(=\) 3cm, BC \(=5cm.\)
Tính diện tích tam giác ABC
Áp dụng định lí Pytago có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{3.4}{2}=6\left(cm^2\right)\)
Đúng 2
Bình luận (2)
Diện tích tam giác ABC là:
( 3. 5 ): 2 = 7.5 ( cm2)
Đ/s:...
Đúng 1
Bình luận (3)
cho tam giác ABC có AB=3cm,AC=4cm. Thì chu vi tam giác ABC=?cm
chu vi tam giác ABC là
( 3 x 4 ) : 2 = 6 cm2
Đúng 0
Bình luận (0)
cho tam giác ABC có AB =3cm AC=4cm BC=5cm. Tính các góc trong tam giác ABC
Xét tam giác ABC : \(AB^2+AC^2=3^2+4^2=5^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A \(\Rightarrow\widehat{A}=90^o\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\\
\Rightarrow\widehat{B}=53^o8'\)
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \Rightarrow\widehat{C}=36^o52'\)
Đúng 2
Bình luận (0)
Theo định lí pytago ta có: \(AB^2+AC^2=BC^2=9+16=BC^2=25\)
⇒ Tam giác ABC vuông tại A ⇒ \(\widehat{A}=90^\circ\)
Theo tỉ lệ thức trong tam giác vuông:
\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}=0,8\approx53^{\circ}\)
\(\widehat{C}=90^{\circ}-53^{\circ}=37^{\circ}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6cm , BH = 3cm . Tính AH , AC , CH.
Đề bài thiếu rồi em, cần nói rõ tam giác này là tam giác gì? Vuông hay không? Và nếu vuông thì vuông tại đâu? H là điểm nào?
Đúng 2
Bình luận (0)
Bổ sung đề: ΔABC vuông tại A, AH là đường cao
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=AC^2-BH^2=6^2-3^2=27\)
hay \(AH=3\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBCA vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{\left(3\sqrt{3}\right)^2}{3}=9\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow AC^2=\left(3\sqrt{3}\right)^2+9^2=108\)
hay \(AC=6\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A90)có đường cao ah . biết Ab3cm và AC4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
Đọc tiếp
cho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBAcho tam giác góc vuông ABC(A=90)có đường cao ah . biết Ab=3cm và AC=4cm.a chứng minh tam giác HBA~ AbC, B tính độ dài BC và AH AbC, B tính độ dài BC và AH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Đúng 0
Bình luận (0)
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC là tam giác đều có AB=3cm. Tính diện tích tam giác ABC
nếu gọi canh là 'a' thì diện tích của tam giác đều là:
(a2*căn 3)/4
do đó diện tích bằng (32*căn 3)/4
hãy k đúng cho mình nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời