có

Xét tam giác ABC có

\(BC^2=AB^2+AC^2\\ \Rightarrow16^2=9^2+12^2\\\Rightarrow256=81+144 \)

=> Tam giác ABC k phải là tam giác vuông

không phải

AB/MN=AC/MP=BC/NP

=>ΔABC đồng dạng với ΔMNP

Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)

\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)

=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)

=> \(DF=\sqrt{144}=12\left(cm\right)\)

Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh

Xét tam giác ABC và tam giác DEF ta có :

\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)

\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)

\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)

=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)

=> Tam giác ABC đồng dạng tam giác DEF

Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được

ko b oi

hai tam giác ko thể đồng dạng bạn nhé

câu 1

A(x)=3x²-5x=0

=>3x²=5x

=>3x=5( chia cả hai vế cho x)

=>x=\(\frac{5}{3}\)

Vậy ...

Câu 2

Vì theo quan hệ giữa canh và ba góc trong một tam giác nên cạnh

 dài nhất nên góc đối diên với nó lớn nhất,cạnh ngắn nhất đối diện với cạnh nhỏ nhất

Ta có AB>BC>AC

=>C>A>B

Vậy ...

nhớ tk mình nha

Đề thiếu rồi bạn

Đề thiếu rồi bạn ơi

* Trong tam giác vuông A’B’C’ có  ∠ A ' = 90 0

Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2

Suy ra:  A ' C ' 2 = B ' C ' 2 - A ' B ' 2  = 15 2 - 9 2  = 144

Suy ra: A’C’ = 12 (cm)

* Trong tam giác vuông ABC có  ∠ A = 90 0

Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2  =100

Suy ra: BC = 10 (cm)

Ta có: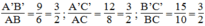 

Suy ra: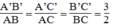 

Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)

Đáp án là B

không nha

vì 6/9 khác 8/15

=> hai tam giác ko đồng dạng

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
   AB² = AH² +  HB² (định lý Py-ta-go)
   20²  = AH² + 16²
   400  = AH² + 256
   AH² = 400 - 256
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   AC² = 12²  + 5²
   AC² = 144  + 25
   AC² = 169
   AC  = \(\sqrt{169}\)= 13 (cm)

Vậy AH = 12 cm
       AC = 13 cm

Bài 2:
Xét tam giác AHC vuông tại H, ta có:
   AC² = AH² + HC² (định lý Py-ta-go)
   15²  = AH² + 9²
   225  = AH² + 81
   AH² = 225 - 81
   AH² = 144
   AH  = \(\sqrt{144}\)= 12 (cm)

Xét tam giác AHB vuông tại, ta có:
   AB² = AH² + HB² (định lý Py-ta-go)
   AB² = 12²  + 5²
   AB² = 144  + 25
   AB² = 169
   AB  = \(\sqrt{169}\)= 13 (cm)

Vậy AB = 13 cm

Câu này dễ

AH 12cm

AC13cm

AB13cm