cho tam giác ABC có góc A= 120o ; AB=6cm
Tính góc A;C ; cạnh AC ; BC
Cho tam giác ABC có A ^ = 120 o . Trên tia phân giác của góc A lấy điểm D sao cho AD=AB+AC. Khi đó tam giác BCD là tam giác gì?
A. cân
B. đều
C. vuông
D. vuông cân
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
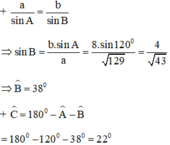
Cho góc xOy có số đo 120o điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox, kẻ AC vuông góc với Oy. Tam giác ABC là tam giác gì ? Vì sao?


Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :

⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)
⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.
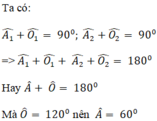
Tam giác cân ABC có góc A = 60º nên là tam giác đều.
Cho tam giác ABC cân tại A, góc B A C ^ = 120 o và AB = 4cm Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
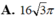
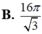
![]()
cho tam giác ABC có Â=50o,C=70o,góc ngoài của tam giác tại đỉnh B là:
A. 140o
B. 1000
C. 60o
D. 120o
Cho tam giác ABC có các góc nhỏ hơn 120o. Ở phía ngoài tam giác ABC, vẽ các tam giác đều ABD và ACE.Gọi I là giao điểm của DC và BE. Tính số đo góc BIC.
Gọi I là giao điểm của AB và DC
và có:
Nên (c.g.c) do đó
Xét và có
(đối đỉnh)
Nên
Vậy
Gọi N thuộc tia đối của ME sao cho thì đều do có và
Xét và có:
Nên và (c.g.c) do đó
Vậy
coppy mạng lỗi hết bài rồi kìa Nam :))
Cho góc xOy có số đo bằng 120o , điểm A thuộc tia phân giác của góc xOy . Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ Ax vuông góc với Oy (C thuộc Oy), tam giác ABC là tam giác gì ? Vì sao ?
Ta có: OA là tia phân giác của \(\widehat{xOy}\)(gt)
nên \(\widehat{xOA}=\widehat{yOA}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
hay \(\left\{{}\begin{matrix}\widehat{BOA}=60^0\\\widehat{COA}=60^0\end{matrix}\right.\)
Ta có: ΔAOC vuông tại C(AC\(\perp\)Oy tại C)
nên \(\widehat{CAO}+\widehat{COA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{CAO}=30^0\)
Ta có: ΔAOB vuông tại B(AB\(\perp Ox\) tại B)
nên \(\widehat{BAO}+\widehat{BOA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Ta có: \(\widehat{CAB}=\widehat{CAO}+\widehat{BAO}\)(tia AO nằm giữa hai tia AB,AC)
\(\Leftrightarrow\widehat{CAB}=30^0+30^0\)
hay \(\widehat{CAB}=60^0\)
Xét ΔAOC vuông tại C và ΔAOB vuông tại B có
AO chung
\(\widehat{CAO}=\widehat{BAO}\left(=30^0\right)\)
Do đó: ΔAOC=ΔAOB(cạnh huyền-góc nhọn)
hay AC=AB(hai cạnh tương ứng)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
Tam giác ABC có các đường phân giác BD và CE cắt nhau tại I trong đó góc BIC bằng 120 o . Số đo góc A là:
A. 60 °
B. 70 °
C. 110 °
D. 50 °
Trong tam giác BIC có ∠(BIC) + ∠(IBC) + ∠(ICB) = 180o ⇒ (IBC) + (ICB) = 60o
∠(ABC) + ∠(ACB) = 2∠(IBC) + 2∠(ICB) = 2(∠(IBC) + ∠(ICB) ) = 2.60o = 120o
Có ∠A = 180o - 120o = 60o. Chọn A
Cho tam giác ABC vuông cân ở A, có A ^ = 120 o . Trên đáy BC lấy hai điểm M,N sao cho BM=CN=AB
Tính số đo góc M A N ^
A. 45 °
B. 30 °
C. 90 °
D. 60 °
Cho khối chóp S . ABC có đáy là tam giác ABC cân tại A, BAC = 120o, AB = a. Cạnh bên SA vuông góc với mặt đáy, SA = a. Thể tích khối chóp đã cho bằng
A. a 3 3 4
B. a 3 3 12
C. a 3 3 2
D. a 3 3 6
Phương pháp:
Sử dụng ![]()
Thể tích khối chóp V = 1 3 h.S với h là chiều cao hình chóp và S là diện tích đáy.
Cách giải:
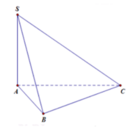
Diện tích đáy SABC = 1 2 AB. AC. sin BAC
![]()
Thể tích khối chóp
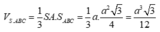
Chọn B.