a: Xét ΔABC có \(BC^2=AB^2+AC^2\)

nên ΔABC vuông tại A

b: Xét ΔAHC vuông tại H có \(\widehat{C}=45^0\)

nên ΔAHC vuông cân tại H

=>\(AH=HC=\dfrac{BC}{2}=\dfrac{5}{2}\sqrt{2}\left(cm\right)\)

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

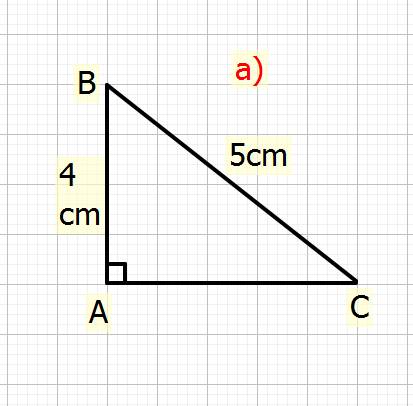
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

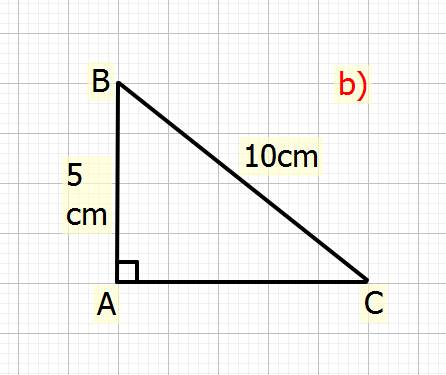
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

Xét tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right)\)

bài 2:

ta có: AB<AC<BC(Vì 3cm<4cm<5cm)

=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)

Bài 3:

*Xét tam giác ABC, có:

       góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)

hay góc A+60 độ +40 độ=180độ

  => góc A= 180 độ-60 độ-40 độ.

  => góc A=80 độ

Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)

        => BC>AC>AB( Các cạnh và góc đối diện trong tam giác)

bài 2:

ta có: AB <AC <BC (Vì 3cm <4cm <5cm)

=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)

Bài 3:

*Xét tam giác ABC, có:

       góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)

hay góc A+60 độ +40 độ=180độ

  => góc A= 180 độ-60 độ-40 độ.

  => góc A=80 độ

Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)

        => BC>AC>AB( Các cạnh và góc đối diện trong tam giác)

HT mik làm giống bạn Dương Mạnh Quyết

S ABC=1/2*AH*BC=1/2*4*5=10cm²

Áp dụng định lí Pytago có:

\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

\(\Rightarrow S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{3.4}{2}=6\left(cm^2\right)\)

Diện tích tam giác ABC là:

( 3. 5 ): 2 = 7.5 ( cm²)

Đ/s:...

Xét tam giác ABC : \(AB^2+AC^2=3^2+4^2=5^2=BC^2\)

\(\Rightarrow\Delta ABC\) vuông tại A \(\Rightarrow\widehat{A}=90^o\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \Rightarrow\widehat{B}=53^o8'\)

\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \Rightarrow\widehat{C}=36^o52'\)

Theo định lí pytago ta có: \(AB^2+AC^2=BC^2=9+16=BC^2=25\)

⇒ Tam giác ABC vuông tại A ⇒ \(\widehat{A}=90^\circ\)

Theo tỉ lệ thức trong tam giác vuông:

\(sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}=0,8\approx53^{\circ}\)

\(\widehat{C}=90^{\circ}-53^{\circ}=37^{\circ}\)

Vì cạnh AC = BC = 5cm nên ∠B = ∠A và cùng là góc lớn nhất. Chọn D

vì Δ ABC có AH \(\perp\)BC ( H thuộc BC)nên AH là đường cao của  Δ ABC

=>\(S_{ABC}=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.5.4=10cm^2\)

= 10 c m 2