Cho đường tròn ( I ; 4 2 ) , cho điểm A thỏa mãn: IA = 2 2 . Hỏi qua điểm A kẻ được bao nhiêu tiếp tuyến đến đường tròn?
A. 1
B. 0
C. 2
D. Vô số
Câu 72. Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB = 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI = 1cm, AO = 4cm, BP = 4cm.
a. Vẽ đường tròn (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?
b. Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c. Vẽ đường tròn (I; 1cm). Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
Cho năm điểm thẳng hàng A, B, I, P, O sao cho đoạn AB = 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI =1cm, AO = 4cm, BP = 4cm.
a) Vẽ đường (O; 2cm). Điểm P có nằm trên đường tròn này không? Vì sao?
b) Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Vẽ đường tròn (I; 1cm)? Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
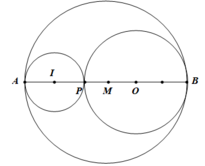
a) Điểm P, O nằm giữa A và B, AO = 4cm, BP = 4cm nên PO = 2cm, BO = 2cm.
Vậy điểm P có nằm trên đường tròn (O; 2cm).
b) Gọi M là trung điểm của AB =>AM = 3cm.
Lại có AI = 1cm => IM = 2cm
=> điểm I nằm trong đường tròn có đường kính AB ( do IM < AM ).
Có OI = 3cm > OP = 2cm nên điểm I nằm ngoài đường tròn (O; 2cm).
Vậy điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O; 2cm).
c) Đường tròn (I; 1cm) tiếp xúc với các đường tròn(O; 2cm) và đường tròn có đường kính AB
vì AP + PB = AB
Cho hai đường tròn (O;4cm), (I;2cm) cắt nhau tại hai điểm phân biệt A, B sao cho OAI ≠ 90o. Tiếp tuyến của đường tròn (O) tại A cắt đường tròn (I) tại C khác A.Tiếp tuyến của đường tròn (I) tại A cắt đường tròn (O) tại D khác A. Gọi E là giao điểm của AB và CD. Gọi P, Q lần lượt là trung điểm của AD, CD. Chứng minh :
a) Hai tam giác APQ, ABC đồng dạng
b) ED = 4EC
giúp em bài này với ạ.
Cho đường tròn (I) tiếp xúc trong với đường tròn (O) tại A . Đường kính AB của đường tròn (O) cắt đường tròn (I) tại điểm thứ hai C khác A . Từ B vẽ tiếp tuyến BP với đường tròn (I) cắt đường tròn (O) tại Q .Chứng minh AP là phân giác của góc IAQ
Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. Hãy cho biết ACBD là hình gì? Vì sao?
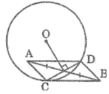
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Cho 5 điểm thẳng hàng A, B, I, P, O sao cho đoạn AB= 6cm, các điểm I, P, O nằm giữa A và B. Cho biết AI=1cm, AO=4cm, BP=4cm
a. Vẽ đường tròn (O;cm). Điểm P có nằm trên đường tròn này không? Vì sao?
b. Chứng tỏ điểm I nằm trong đường tròn có đường kính AB và nằm ngoài đường tròn (O;2cm)
c. Vẽ đường tròn (I=1cm). Đường tròn này tiếp xúc các đường tròn nào? Vì sao?
GIẢI ĐẦY ĐỦ CHI TIẾT VÀ DỄ HIỂU CHO MÌNH NHA. AI NHANH ĐƯỢC LIKE
Số học sinh lớp 6A và lớp 6B là 2/3 hay là 8/12
Khi tăng số học sinh lớp 6A thêm 8 bạn, lớp 6B lên 4 bạn thì tỉ số là 3/4 hay là 9/12
vậy lớp 6 A thêm số học sinh hơn lớp 6B là 8 - 4 = 4 bạn
4 bạn ứng với số phần là: 9/12 - 8/12 = 1/12
Lớp 6A có số học sinh là: 4x 12 - 8 = 40 (hs)
Lớp 6B có số học sinh là: 40x 3 : 2= 60 (hs)
Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm bên ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. Hãy cho biết ACBD là hình gì ? Vì sao ?
cho đường tròn tâm O và đường tròn tâm I cắt nhau tại A và B.Tiếp tuyến tại A của đường tròn tâm O và đường tròn tâm I cắt đường tròn tâm I và O lần lượt tại D và C.a,Chứng minh AD²=BC×BD.b,Tam giác BDI là tam giâc cân
b: Xét ΔIBD co IB=ID
nên ΔIBD cân tại I
cho đường tròn (O;OA),điểm I thuộc bán kính OA sao cho AI=1/3 OA.vẽ đường tròn (I;IA).
a)Xác định vị trí của hai đường tròn (O) và (I)
b)kẻ một đường thẳng qua A,cắt các đường tròn (I) và (O) theo thứ tự ở B và C.tính tỉ số AB/AC
Cho tam giác nhọn ABC (AB<AC) ngoại tiếp đường tròn tâm I. Đường tròn (I) tiếp xúc với các cạnh BC,CA,AB lần lượt tại D,E,F. Đường thẳng EF cắt đường thẳng BC tại M. Đường thằng AD cắt đường tròn (I) tại N(khác D). Chứng minh MN là tiếp tuyến của đường tròn (I).