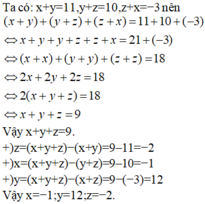tìm các số x,y,z biết; 2x\3=3y\4=4z\5 và x+y+z=49

Những câu hỏi liên quan
1. Tìm các số x, y, z biết rằng:\(\frac{x}{5}=\frac{y}{6},\frac{y}{8}=\frac{z}{7}\) và x + y - z = 69
2. Tìm các số x, y, z biết rằng: \(\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}\) và 5z - 3x - 4y = 50
3. Tìm các số x, y, z, t biết rằng:
x: y: z : t = 15: 7 :3 :1 và x - y + z - t = 10
1, ta co \(\frac{x}{5}=\frac{y}{6}=\frac{x}{20}=\frac{y}{24}\)
\(\frac{y}{8}=\frac{z}{7}=\frac{y}{24}=\frac{z}{21}\)
=>\(\frac{x}{20}=\frac{y}{24}=\frac{z}{21}=\frac{x+y-z}{20+24-21}=\frac{69}{23}=3\)
=>\(x=3\cdot20=60\)
\(y=3\cdot24=72\)
\(z=3\cdot21=63\)
Đúng 0
Bình luận (0)
3. ta co \(\frac{x}{15}=\frac{y}{7}=\frac{z}{3}=\frac{t}{1}=\frac{x+y-z+t}{15-7+3-1}=\frac{10}{10}=1\)
=> \(x=1\cdot15=15\)
\(y=1\cdot7=7\)
\(z=1\cdot3=3\)
\(t=1\cdot1=1\)
Đúng 0
Bình luận (0)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{5}=\frac{y}{7}=\frac{z}{9}=\frac{x-y+z}{5-7+9}=\frac{315}{7}=45\)
suy ra: x/5 = 45 => x = 225
y/7 = 45 => y = 315
z/9 = 45 => z = 405
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a)Tìm x,y thuộc z biết rằng (y+1).(xy-1)=3
b)tìm các số x,y,z biết rằng x+y=2 ;y+z=3 ;z+x=-5
Tìm các số x, y, z biết: x + y = 2, y + z = 5, z + x = -3
Tìm các số x,y,z biết: x + y 11, y + z 10, z + x - 3 A. x−1;y12;z−2. B. x−1;y11;z−2. C. x−2;y−1;z12. D. x12;y−1;z−2
Đọc tiếp
Tìm các số x,y,z biết: x + y = 11, y + z = 10, z + x = - 3
A. x=−1;y=12;z=−2.
B. x=−1;y=11;z=−2.
C. x=−2;y=−1;z=12.
D. x=12;y=−1;z=−2
tìm các số nguyên x ,y, z biết x + y =2 y+z=3 z+x = -5
\(x\) + y = 2; ⇒ y = 2 - \(x\);
y + z = 3 ⇒ y = 3 - z
⇒ 2 - \(x\) = 3 - z ⇒ \(x\) = 2 - 3 + z ⇒ \(x\) = -1 + z
Thay \(x\) = -1 + z vào biểu thức z + \(x\) = -5 ta có:
z - 1 + z = -5
2z = -5 + 1 ⇒ 2z = -4 ⇒ z = -4: 2 ⇒ z = -2
Thay z = -2 vào biểu thức \(x\) = -1 + z ta có \(x\) = -1 -2 = -3
Thay z = -2 vào biểu thức y = 3 - z ta có: y = 3 - (-2) = 5
Đúng 0
Bình luận (0)
5) tìm các số x,y,z biết : y+x+1/x = x+z+2/y = 1/x+y+z
1) Cho x, y, z là ba số dương phân biệt. Hãy tìm tỉ số x/y ,biết rằng:
y/x-z=x+y/z=x/y
2) Tìm các số x, y, z , biết rằng
x-1/2=y+3/4=z-5/6 và 5z-3x-4y=50
Cho x, y, z là 2 số nguyên dương biết rằng tổng các chữ số của x bằng tổng các chữ số của y, tổng các chữ số của y bằng tổng các chữ số của z và x+y+z=60. Tìm x, y, z
tìm các số hữu tỉ x,y,z biết rằng:x(x+y+z)=-5:y(x+y+z)=9;z(x+y+z)=5.
mình sẽ đơn giản cách giải ấy cho cậu
cậu lần lượt cộng các vế trái và xế phải lại thì ta sẽ được (x + y + z)(x + y + z) = -5 + 9 + 5
(x + y + z)2 = 9
chắc bạn học qua lũy thừa rồi nhỉ, thì ta sẽ có được 9 = 32 hoặc 9 = (-3)2
vậy có 2 trường hợp hoặc (x + y + z) = 3 hoặc (x + y + z) = -3
với (x + y + z) = 3 thì thay vào x (x + y + z) = -5 => 3x = -5 => x = \(\frac{-5}{3}\)
tương tự ,cậu thay (x + y + z) = 3 vào vao 2 biểu thức còn lại ta sẽ được y = 3, z = \(\frac{5}{3}\)
Và trường hợp còn lại (x + y + z) = -3 cậu cũng thay lần lượt vào 3 biểu thức trên, ta sẽ suy ra được
x = \(\frac{5}{3}\) ; y = -3 ; z= \(\frac{-5}{3}\)
vậy \(\orbr{\begin{cases}x=\frac{-5}{3};y=3;z=\frac{5}{3}\\x=\frac{5}{3};y=-3;z=\frac{-5}{3}\end{cases}}\) thế nhé, mình lười viết đầy đủ phần trên cho nên neesuko hiểu cứ hỏi mình
Đúng 0
Bình luận (0)
\(\hept{\begin{cases}x\left(x+y+z\right)=-5\left(1\right)\\y\left(x+y+z\right)=9\left(2\right)\\z\left(x+y+z\right)=5\left(3\right)\end{cases}}\)
Cộng theo vế của (1), (2) và (3) ta đc:
\(\left(x+y+z\right)^2=9=\left(-3\right)^2\)hoặc\(3^2\)
\(\Rightarrow x+y+z=-3\)hoặc\(3\)
Xét \(x+y+z=3\)lần lượt thay vào (1), (2), (3) ta có:
\(\hept{\begin{cases}x=-\frac{5}{3}\\y=3\\z=\frac{5}{3}\end{cases}}\)
Xét \(x+y+z=-3\)cũng thay vào (1),(2),(3) đc:
\(\hept{\begin{cases}x=\frac{5}{3}\\y=-3\\z=-\frac{5}{3}\end{cases}}\)
Vậy....
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm các số hữu tỉ x,y,z biết rằng:x(x+y+z)=-5;y(x+y+z)=9;z(x+y+z)=5