Cho hai tập hợp M = { 0; 2 ; 4;....102; 104; 106 }
Q = { x E N* | x là số chẵn, x < 106 }
a) Mỗi tập hợp có bao nhiêu phần tử ?
b) Dùng kí hiệu tập hợp con để thực hiện mối quan hệ giữa M và Q
Cho hai tập hợp M = {0} và N = ∅ . Hỏi tập N có phải là tập hợp con của tập M hay không?
Cho hai tập hợp M = {0} và N = ∅ . Hỏi tập N có phải là tập hợp con của tập M hay không?
Cho hai tập hợp M = {0} và N = ∅ . Hỏi tập N có phải là tập hợp con của tập M hay không?
Cho tập hợp A = (0;+ ∞ )và B={ x ϵ R | mx2 - 4x+ m-3 = 0 }. Tìm m để B có đúng hai tập con và B ⊂ A
Cho hai tập hợp \(A=\left(0;+\infty\right)\) và \(B=\left\{x\in R|mx^2-4x+m-3=0\right\}\). Tìm m để B có đúng 2 tập hợp con và \(B\subset A\)
\(mx^2-4x+m-3=0\left(1\right)\)
Để tập hợp B có đúng 2 tập con và \(B\subset A\) thì \(\left(1\right)\) có 2 nghiệm phân biệt cùng dương
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\P>0\\S>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-m\left(m-3\right)>0\\\dfrac{m-3}{m}>0\\\dfrac{4}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-4< 0\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 4\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow3< m< 4\)
Ta có:
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}\)
+) \(\overrightarrow{BG}=\dfrac{1}{3}\left(\overrightarrow{BM}+\overrightarrow{BN}\right)=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CN}\right)\)
\(=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{DC}\right)=\dfrac{1}{3}\left(-\dfrac{13}{6}\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\dfrac{13}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
=> \(\overrightarrow{AG}=\dfrac{5}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Mặt khác:
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}=\overrightarrow{AB}+k\overrightarrow{BC}=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
Để A, G, I thẳng hàng
=>\(\dfrac{\dfrac{5}{18}}{1-k}=\dfrac{\dfrac{1}{3}}{k}\Rightarrow k=\dfrac{6}{11}\)
Cho hai tập hợp A = {0; 2} và B = {0; 1; 2; 3; 4}. Có bao nhiêu tập hợp X thỏa mãn A ∪ X = B?
Cho tập hợp A = {0 ; -3 ; 5}. Viết tập hợp B các phân số m/n mà m, n ∈ A. (Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số)
Gợi ý:
Ta lấy số đầu làm tử, chính số đó và hai số còn lại làm mẫu, tiếp đến lấy số thứ hai làm tử, hai số kia làm mẫu ... (loại các phân số có mẫu bằng 0).
Lời giải
Ta có: Mẫu số của một phân số phải khác 0.
Do đó m có thể chọn trong các số 0; -3; 5.
n có thể chọn trong các số -3; 5.
Vậy ta có thể viết được các phân số 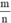 là:
là:
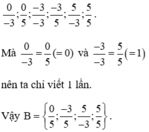
1)Cho M là tập hợp các chữ số lẻ. Số tập con của M chỉ gồm hai phần tử là ...
2)Tổng của hai số bằng 180. Thương của phép chia số lớn cho số bé bằng 5. Tích hai số ấy là ...
3)Cho A là tập hợp các số tự nhiên trong đó có chứa chữ số 0 và B là tập hợp các số tự nhiên có dạng a0b. Tập hợp C gồm các phần tử vừa thuộc A vừa thuộc B. Tập hợp C có số phần tử là ...
bài 1=10
Bài 2=4500
Bài 3=90
Chắc chắn ở vòng 5 lớp 6
)gọi N là con của M
M $\supset$⊃N= [ 3;5 ]
2) gọi số lớn là a, số bé là b ta có a+b= 180
=> a/5= b/1
tổng số phần bằng nhau là 5+1=6
=> b= 180:6= 30
=> a= 30. 5 = 150
Cho tập hợp A = { 0; -3; 5 }. Viết tập hợp B các phân số m/n mà m,n thuộc A. ( Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số)
Vì m và n thuộc 0;-3;5 nên n phải khác 0 ( vì m./n là phân số )
Ta có các phân số đó là \(-\frac{3}{5};\frac{0}{3};\frac{0}{5};-\frac{5}{3}\)
Do đó ta có tập hợp \(\left\{\frac{-3}{5};\frac{-5}{3};\frac{0}{5};\frac{0}{3}\right\}\)
Vậy \(B=\left\{-\frac{3}{5};-\frac{5}{3};\frac{0}{3};\frac{0}{5}\right\}\)
\(B=\left\{\frac{0}{-3};\frac{0}{5};\frac{-3}{5};\frac{5}{-3}\right\}\)
Vì 0 không thể là mẫu số nên các phân số phải tìm chỉ có thể có mẫu bằng - 3 hoặc 5.
Các phân số có mẫu bằng -3 là : 0/-3 ; -3/-3 ; 5/-3
Các phân số có mẫu bằng 5 là: 0/5 ; -3/5 ; 5/5
Nhưng 0/−3=0=0/5,−3/−3=1=5/5
Vậy chỉ có bốn phân số khác nhau: 0, 1, 5/−3,−3/5
Cho M = {x ∈ R : mx2 - 4x + m - 3 = 0, m ∈ R}. Số giá trị của m để M có đúng hai tập hợp con là:
A. 0.
B. 1
C. 2
D. 3
Đáp án: D
M có hai tập hợp con => tập hợp M có 1 phần tử
=> phương trình mx2 - 4x + m - 3 = 0 có một nghiệm.
TH1: m = 0. Phương trình có 1 nghiệm x = -3/4.
TH2: m ≠ 0. Phương trình có 1 nghiệm khi
Δ' = 4 - m(m + 3) = -m2 + 3m + 4 = 0 => m = 4; m = -1