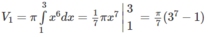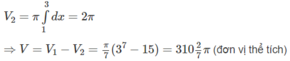Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = ln x , y = 0 , x = 2  quanh trục Ox là:

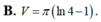
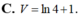
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0,  x   =   π 3 quanh Ox là:

A.  3 - π 3

B.  π 3 - 3

C.  π 2 3 - π 3

D.  π 3 - π 2 3

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = x 2 ; y=0; x=1; x=2 quanh trục Ox là

A.  5 π 12

B.  π 12

C.  7 π 12

D.  3 π 12

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = x 2 , y = 0 , x = 1 ,   x = 2  quanh trục Ox là

A. 5 π 12

B.  3 π 12

C.  7 π 12

D.  π 12

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = lnx , y = 0, x = 1, x = 2 quanh trục Ox là

A. V = πln 2

B.  V = π ln 4 − 1

C.  V = ln 4 + 1

D.  V = π 2 − ln 4

Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y   =   x 3 ; y=0; x=0; x=1 quanh trục hoành bằng

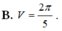
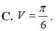
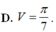
Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường  y = x 3 , y = 0 , x = 0 , x = 1 quanh trục hoành bằng

A. V =  π 4

B. V =  2 π 5

C. V =  π 6

D. V =  π 7

Thể tích vật thể tròn xoay khi quay hình phẳng  H  giới hạn bởi các đường  y = x 3 ,   y = 0 ,   x = 0 ,   x = 1  quanh trục hoành bằng

A.  V = π 4

B.  V = 2 π 5

C.  V = π 6

D.  V = π 7