Bài 3: Cho (d1): y = -2x ; (d2): y = x – 3 ; (d3): y = mx + 4 a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 b) Tìm các giá trị tham số m để 3 đường thẳng d1, d2, d3 đồng quy.

Những câu hỏi liên quan
BÀI 12:
CHO 3 ĐƯỜNG THẲNG d1 y=2x+1,d2 y=3x-1 và d3 y=x+3
CM: d1,d2,d3 đồng quy
PT hoành độ giao điểm \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(2x+1=3x-1\Leftrightarrow x=2\Leftrightarrow y=5\Leftrightarrow A\left(2;5\right)\)
Thay \(x=2;y=5\) vào \(\left(d_3\right)\Leftrightarrow2+3=5\) (đúng)
Do đó \(A\left(2;5\right)\in\left(d_3\right)\)
Vậy \(\left(d_1\right);\left(d_2\right);\left(d_3\right)\) đồng quy tại \(A\left(2;5\right)\)
Đúng 1
Bình luận (1)
\(\left\{{}\begin{matrix}2x+1=3x-1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=5\end{matrix}\right.\)
Thay x=2 và y=5 vào y=x+3, ta được:
2+3=5(đúng)
Đúng 1
Bình luận (0)
Bài 1: Cho hai đường thẳng (d1):y = -2x + 1 và (d2):y = (2m - 3)x + 3 - m. Tìm m để (d1) cắt (d2) tại điểm có tung độ bằng 3.
Do giao điểm có tung độ bằng 3 nên hoành độ thỏa mãn:
\(3=-2x+1\Rightarrow x=-1\)
Thế tọa độ giao điểm vào pt d2 ta được:
\(3=-\left(2m-3\right)+3-m\)
\(\Rightarrow-3m+3=0\Rightarrow m=1\)
Đúng 4
Bình luận (0)
Bài 1: cho 2 đường thẳng y=(m-3)x+3 (d1) và y= -x+m (d2). Tìm m để (d1)// (d2)
Bài 2: cho 2 đường thẳng y=2x (d1) và y= -x+3 (d2)
a) tìm tọa độ giao điểm A của (d1) và (d2)
b) viết phương trình đường thẳng (d3) qua A và // với đường thẳng y= x+4 (d)
Giải chi tiết dùm mình với ạ :<
BÀI 1
để d1 và d2 // thì: m-3=-1(1) ; m khác 3 (2)
ta có: (1) <=> m=2 (3)
từ (2) và (3) => để d1//d2 thì m = 2
Đúng 0
Bình luận (0)
Cho đường thẳng d: y=-2x+1 và và d cắt Ox tại A, d cắt Oy tại B. Hãy tính:
a) Từ O đến d b) Diện tích tam giác AOB
Bài 4: Cho đường thẳng d1: y = 2x – 3 và d2: y = -3x + 7.
a) Vẽ d1, d2 trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của d1, d2.
Bài 5: Cho hai đường thẳng d: y = -3x + 1 và d’: y = -x – 2. Tìm tọa độ giao điểm của d và d’.
Bài 1:Xác định m để ba đường thẳng sau: 1: y -2x, d2: y -x +1, d3 : y -(m +3)x - 2m +1 đồng quy.Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y -2x và d2 : y x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Đọc tiếp
Bài 1:Xác định m để ba đường thẳng sau:
1: y= -2x, d2: y = -x +1, d3 : y = -(m +3)x - 2m +1 đồng quy.
Bài 2: Trên cùng một mặt phẳng tọa độ cho hàm số d1 : y = -2x và d2 : y = x+3. a) Tìm tọa độ giao điểm của hai đường thẳng d1 và d2 bằng hai cách.
b) Viết phương trình đường thẳng d3 biết đường thẳng này song song với d1 và cắt d2 tại điểm có hoành độ bằng 1.
Bài 3 :Xác định các hệ số a, b biết đường thẳng d: y ax +b song song với đường thẳng d1 : y = 3.x và cắt trục hoành tại điểm có hoành độ bằng 2/3
Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2
Đúng 0
Bình luận (1)
Cho hai đường thẳng (d1):y = -2x + 1 và (d2):y = (2m - 3)x + 3 - m. Tìm m để (d1) cắt (d2) tại điểm có tung độ bằng 3. Giá trị của m là:...
Mong các CTV giải bài này giúp mình! Cảm ơn các bạn!
bài này dễ mà bạn :
\(d_1,d_2\)cắt nhau tại diểm có tung độ là 3 nên hoành độ của giao điểm là :
(thay \(y=3\)vào \(d_1\)) \(3=-2x+1\Leftrightarrow-2x=2\Leftrightarrow x=-1\)Tọa độ của giao điểm cũng thỏa mãn phương trình \(d_2\)nên: \(3=-\left(2m-3\right)+3-m\Leftrightarrow-3m=-3\)\(\Leftrightarrow m=1\)
Đúng 1
Bình luận (0)
Bài 1: Cho ( d1 ) y -x+ma) Tìm m để đồ thị hàm số đi qua B nằm trên trục hoành có hoành độ -1b) Vẽ ( d1 ) với giá trị m vừa tìm được ở câu a c) Tìm để ( d1 ) đồng qui với ( d2 ) y 2x - 2 và ( d3 ) y -x + 4Bài 2: Cho ( d1 ) y x - 1 ; ( d2 ) y -2x +2 a) Vẽ ( d1 ) và ( d2 ) trên cùng một mặt phẳngb) Tìm tọa độ giao điểm của ( d1 ) và ( d2 ) bằng phép toánc) Biết ( d3 ) y ( ^{m^2}- 2 )x + đồng qui với ( d1 ) và ( d2 ). Tìm m
Đọc tiếp
Bài 1: Cho ( d1 ) y= -x+m
a) Tìm m để đồ thị hàm số đi qua B nằm trên trục hoành có hoành độ = -1
b) Vẽ ( d1 ) với giá trị m vừa tìm được ở câu a
c) Tìm để ( d1 ) đồng qui với ( d2 ) y= 2x - 2 và ( d3 ) y= -x + 4
Bài 2: Cho ( d1 ) y= x - 1 ; ( d2 ) y= -2x +2
a) Vẽ ( d1 ) và ( d2 ) trên cùng một mặt phẳng
b) Tìm tọa độ giao điểm của ( d1 ) và ( d2 ) bằng phép toán
c) Biết ( d3 ) y= ( \(^{m^2}\)- 2 )x + đồng qui với ( d1 ) và ( d2 ). Tìm m
2:
a: 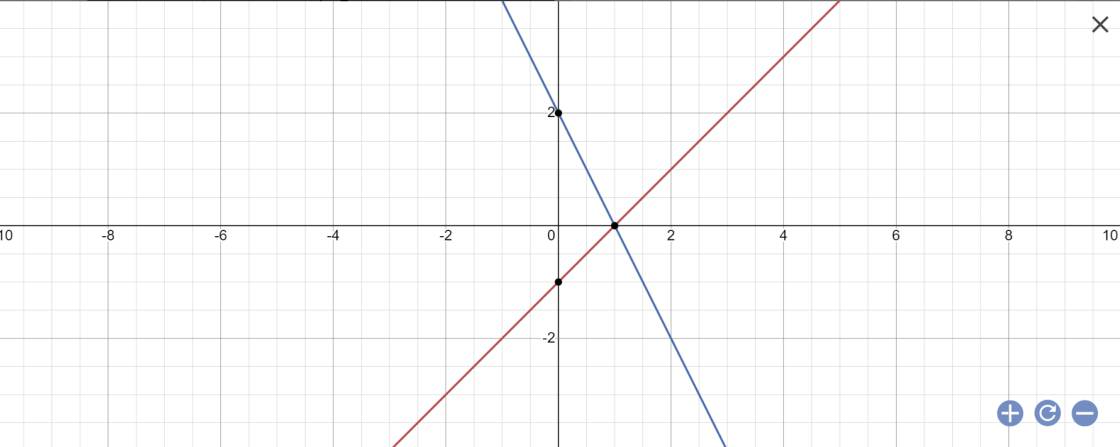
b: Tọa độ giao điểm là nghiệm của hệ:
x-1=-2x+2 và y=x-1
=>3x=3 và y=x-1
=>x=1 và y=1-1=0
1:
a: Thay x=-1 và y=0 vào (d), ta được:
m+1=0
=>m=-1
c: tọa độ giao điểm là:
2x-2=-x+4 và y=2x-2
=>3x=6 và y=2x-2
=>x=2 và y=4-2=2
Thay x=2 và y=2 vào (d), ta được:
m-2=2
=>m=4
Đúng 0
Bình luận (0)
Cho (d): y= (m-1)x + m (d1): y= 2x - 3 Vẽ (d) và (d1) với m=3 và tính khoảng cách (d) và (d1)
Khi m=3 thì (d): y=2x+3
Lấy A(0;3) thuộc (d)
(d1): y=2x-3
=>2x-y-3=0
\(h\left(A;d1\right)=\dfrac{\left|0\cdot2+\left(-1\right)\cdot3+\left(-3\right)\right|}{\sqrt{2^2+1^2}}=\dfrac{6}{\sqrt{5}}\)
Đúng 0
Bình luận (0)
Bài 1. Cho ba đường thẳng(d1): y x + 2,(d2): y -x - 2,(d3): y −2x + 2, (d1) cắt (d2) tại A; (d1) cắt(d3) tại B, (d2) cắt (d3) tại C. a) Xác định tọa độ của các điểm A, B, C.b) Tính diện tích tam giác ABC.giúp mik gải bài này vs mik đag cần gấp
Đọc tiếp
Bài 1. Cho ba đường thẳng
(d1): y = x + 2,
(d2): y = -x - 2,
(d3): y = −2x + 2, (d1) cắt (d2) tại A; (d1) cắt
(d3) tại B, (d2) cắt (d3) tại C.
a) Xác định tọa độ của các điểm A, B, C.
b) Tính diện tích tam giác ABC.
giúp mik gải bài này vs ![]()
![]() mik đag cần gấp
mik đag cần gấp
a: Tọa độ A là:
\(\left\{{}\begin{matrix}x+2=-x-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=-4\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2+2=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x+2=-2x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}-x-2=-2x+2\\y=-x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=-4-2=-6\end{matrix}\right.\)
Vậy: A(-2;0); B(0;2); C(4;-6)
b: \(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(4+2\right)^2+\left(-6-0\right)^2}=6\sqrt{2}\)
\(BC=\sqrt{\left(4-0\right)^2+\left(-6-2\right)^2}=\sqrt{4^2+8^2}=4\sqrt{5}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=0\)
=>\(\widehat{BAC}=90^0\)
=>ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\sqrt{2}\cdot6\sqrt{2}=12\)
Đúng 2
Bình luận (1)

















