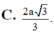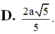Cho hình chóp S.ABCD có tam giác SAB cân tại S, đáy là hình vuông cạnh a, (SC;(ABCD))=45°. Tính
a) d(A;(SCD))
b) d(M;(SCD)) với M là trung điểm của SA
Những câu hỏi liên quan
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là
a
3
15
6
. Góc giữa đường thẳng SC và mặt phẳng đáy(ABCD) là A. 30° B. 45° C. 60° D. 120°
Đọc tiếp
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là a 3 15 6 . Góc giữa đường thẳng SC và mặt phẳng đáy(ABCD) là
A. 30°
B. 45°
C. 60°
D. 120°
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là
a
3
15
6
Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là A.
30
0
B.
45...
Đọc tiếp
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là a 3 15 6 Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là
A. 30 0
B. 45 0
C. 60 0
D. 120 0
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng Thể tích khối chóp S.ABCD bằng A.
a
3
3
12
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng đáy bằng Thể tích khối chóp S.ABCD bằng
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
Chọn đáp án D
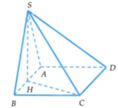
Gọi H là trung điểm của AB. Từ giả thiết ta có S H ⊥ A B C D
Suy ra 
⇒ S H C vuông cân tại H.
Do ∆ B H C vuông tại H nên
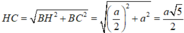
⇒ S H = H C = a 5 2
Thể tích khối chóp V S . A B C D = 1 3 S H . S A B C D = a 3 5 6 đ v t t là
Đúng 0
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng
45
o
. Thể tích khối chóp S.ABCD bằng: A.
a
3
3
12
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng 45 o . Thể tích khối chóp S.ABCD bằng:
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
Chọn D
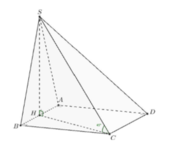
Gọi H là trung điểm của AB.
Do đó:
Xét tam giác vuông BHC:
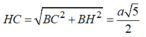
Xét tam giác vuông SHC:
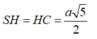
Suy ra:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng
45
°
. Thể tích khối chóp S.ABCD bằng: A.
a
3
3
12
B.
a
3
3...
Đọc tiếp
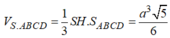
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa đường thẳng SC và mặt phẳng đáy bằng 45 ° . Thể tích khối chóp S.ABCD bằng:
A. a 3 3 12
B. a 3 3 9
C. a 3 5 24
D. a 3 5 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, tam giác SAB cân tại S. SA=SB=2a, (SAB) \(\perp\) (ABCD)
a, Tính (SD,(ABCD))
b, (SH, (SCD)) với H là trung điểm của
c, (SC, (SAB))
d, (SA, (SBC))
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc 450, tam giác SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của hình chóp S.ABCD là: A.
a
3
2
B.
a
3
6
C.
a
3
2
2
D....
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc = 450, tam giác SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích của hình chóp S.ABCD là:
A. a 3 2
B. a 3 6
C. a 3 2 2
D. a 3 2 12
Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 3a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng
60
°
. A.
V
S
.
A
B
C
D
18
a
3...
Đọc tiếp
Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 3a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và (ABCD) bằng 60 ° .
A. V S . A B C D = 18 a 3 15
B. V S . A B C D = 18 a 3 3
C. V s . A B C D = 9 a 3 15 2
D. V S . A B C D = 9 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt bên SAB là tam giác vuông cân tại S và nằm trên mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC A.
a
3
3
.
B.
a
5
5
.
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt bên SAB là tam giác vuông cân tại S và nằm trên mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC
A. a 3 3 .
B. a 5 5 .
C. 2 a 3 3 .
D. 2 a 5 5 .
Đáp án D
Phương pháp giải: Dựng hình, xác định khoảng cách giữa hai đường thẳng thông qua mặt phẳng song song với đường thẳng
Lời giải:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt bên SAB là tam giác vuông cân tại S và nằm trên mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC.
Đọc tiếp
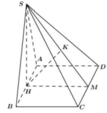
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt bên SAB là tam giác vuông cân tại S và nằm trên mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SC.
