Hình chóp tam giác đều SABC có AB = a, (SC;(ABC)) = 60 ° . Tính thể tích V của SABC
A. V = a 3 4
B. V = a 3 3 12
C. V = a 3 3 4
D. V = a 3 12
cho hình chóp sabc có sa=sb=sc=2a, tam giác vuông tại a có ab=a/2, bc=a. tính thể tích khối chóp sabc
\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)
cho hình chóp sabc có sa=sb=sc=2a, tam giác abc đều cạnh a. tính thể tích khối chóp sab
Gọi H là tâm đáy \(\Rightarrow SH\perp\left(ABC\right)\)
Ta có: \(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{33}}{3}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{33}}{3}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{11}}{12}\)
Cho hình chóp SABCD có SA vuông góc với đáy. Tính thể tích khối chóp SABC biết: a. Tam giác ABC đều cạnh a, góc giữa SB và đáy là 30°. b. Tam giác ABC vuông tại A, AB=a, SA=5a; góc giữa SC và đáy là 60°
Cho hình chóp SABCD có SA vuông góc với đáy. Tính thể tích khối chóp SABC biết: a. Tam giác ABC đều cạnh a, góc giữa SB và đáy là 30°. b. Tam giác ABC vuông tại A, AB=a, SA=5a; góc giữa SC và đáy là 60°
Giải giúp mình:cho hình chóp SABC có đáy là tam giác đều cạnh 2a, hình chiếu của S lên ABC là trung điểm AB. Góc giữa SC và (ABC) là 60°. Tính VSABC/a³ là
a,Tính góc giữa SC và ( ABC)
b, Tính góc giữa ( SBC ) Và ( ABC)
Biết:
1,Hình chóp SABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 30 độ
2, Hình chóp SABC có đáy ABC là tam giác đều , mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA= \(a\sqrt{3}\), SB= a
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, AB=4cm Tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABC) .M thuộc SC sao cho C M = 2 M S . Khoảng cách giữa hai đường A C v à B M là ?
A. 4 21 21 c m
B. 8 21 21 c m
C. 2 21 3 c m
D. 4 21 7 c m
Đáp án là D.
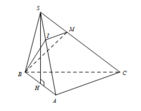
Gọi I là điểm thuộc SA sao cho S I S A = 1 3 ⇒ I M // A C .
Gọi H là trung điểm của .AB S A B ⊥ A B C S A B ∩ A B C = A B S H ⊥ A B ⇒ S H ⊥ A B C
A C ⊥ A B A C ⊥ S H ⇒ A C ⊥ S A B ⇒ I M ⊥ S A B ⇒ I M ⊥ B I ⇒ Δ B I M
V S B A M V S B A C = S M S C = 1 3 ⇒ V S B A M = 1 3 V S B A C = 1 3 . 1 3 S H . S △ A B C = 1 9 . 4 3 2 1 2 A B . A C = 4 3 9 A C
V A B I M V A B S M = A I A S = 2 3 ⇒ V A B I M = 2 3 V A B S M = 2 3 . 4 3 9 A C = 8 3 27 A C
B I 2 = A B 2 + A I 2 − 2 A B . A I . c os 60 0 = 4 2 + 8 3 2 − 2.4. 8 3 . c os 60 0 = 112 9 ⇒ B I = 4 7 3
S Δ B I M = 1 2 B I . I M = 1 2 . 4 7 3 . 1 3 A C = 2 7 9 A C
V A B I M = 1 3 S △ B I M . d A , B I M ⇒ d A , B I M = 3 V A B I M S △ B I M = 3. 8 3 27 A C 2 7 9 A C = 4 21 7
Hình chóp tam giác đều SABC có đáy là tam giác đều ABC, AB = a; góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của hình chóp.
A. V = a 3 12
B. V = a 3 2 24
C. V = a 3 3 16
D. V = a 3 6 36
Cho hình chóp SABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác đều cạnh a 3 , B C = a 3 , đường thẳng SC tạo với mặt phẳng (ABC) góc 60 0 . Thể tích của khối chóp SABC bằng:
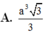
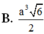
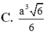
![]()