Cảnh báo
Bạn cần đăng nhập mới làm được đề thi này
Cho hàm số \(y=f\left(x\right)\) với tập xác định \(D=\left[a;c\right]\) có đồ thị :
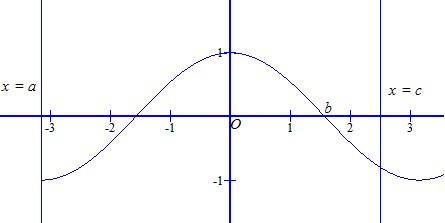
Trong các khẳng định sau, khẳng định nào đúng ?
- Hàm số đã cho là hàm số chẵn
- Đồng biến trong (a;0) và (b;c); nghịch biến trong (0;b)
- Nếu \(a< x_1< x_2< b\) thì \(\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}< 0\)
- Nghịch biến trong khoảng (0; c)
Cho hàm số \(y=f\left(x\right)\) xác định liên tục trên R và có bảng biến thiên sau :
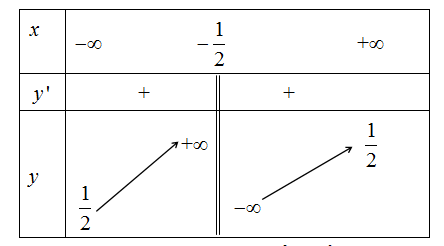
Đường nào trong các đường sau đây có thể là đồ thị của hàm số đã cho ?
- Hình 1
- Hình 2
- Hình 3
- Hình 4
Hướng dẫn giải:
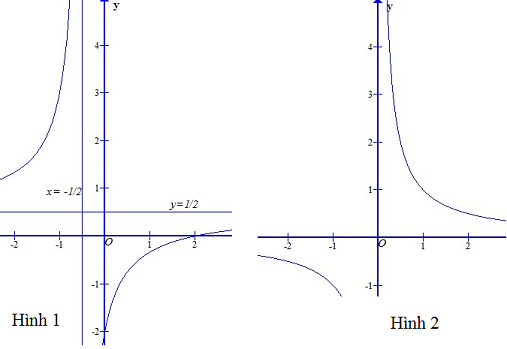
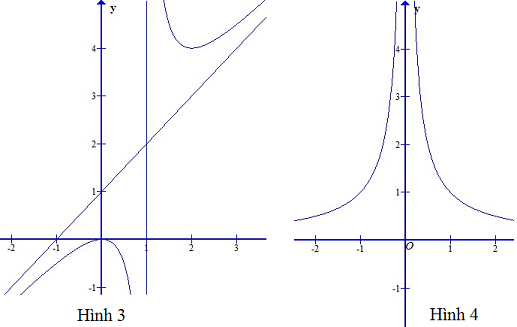
Từ bảng biến thiên thấy đồ thị đã cho có tiệm cận đứng \(x=-\dfrac{1}{2}\) và tiệm cận ngang \(y=\dfrac{1}{2}\).
Trong các khoảng sau đây, hàm số \(y=\ln x^4\) đồng biến trên khoảng nào ?
- \(\left(-\infty;+\infty\right)\)
- \(\left(-\infty;0\right)\)
- \(\left(0;+\infty\right)\)
- \(\left(-1;1\right)\)
Hướng dẫn giải:
Hàm số \(y=lnx^4\) có \(y'=\dfrac{4x^3}{x^4}=\dfrac{4}{x}\) dương trong khoảng \(\left(0;+\infty\right)\); âm trong khoảng \(\left(-\infty;0\right)\)
Trong các đường cong cho sau đây, đường nào là đồ thị của hàm số \(y=\frac{1}{3}x^3-\frac{1}{2}x^2-2x+2\) ?
- Hình 1
- Hình 2
- Hình 3
- Hình 4
Hướng dẫn giải:
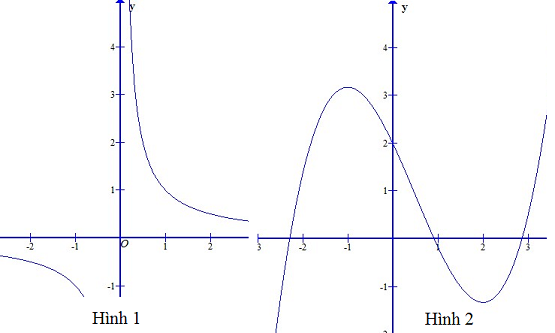
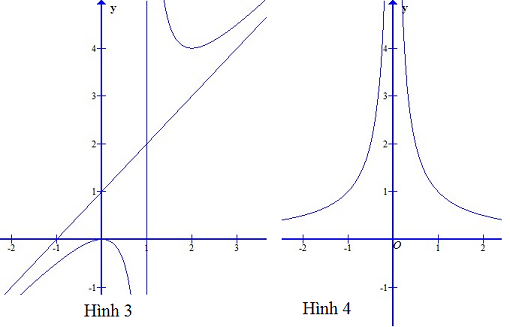
Hàm số đã cho không có tiệm cận, Hình 2 là phù hợp.
Tìm các giá trị cực đại của hàm số \(y=\cos x+\sin x\) .
- \(\sqrt{2}\)
- \(x=\dfrac{\pi}{4}+k\pi\left(k\in \mathbb{Z}\right)\)
- \(-\sqrt{2}\)
- \(x=\dfrac{\pi}{4}+k2\pi\left(k\in \mathbb{Z}\right)\)
Hướng dẫn giải:
Hàm số \(y=\cos x+\sin x=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)\) tuần hoàn, liên trục trên toàn trục số và có GTLN=\(\sqrt{2},\)GTNN=\(-\sqrt{2}\) cũng đồng thời là giá trị cực đại, cực tiểu. Vậy giá trị cực đại là \(\sqrt{2}.\)
Tìm giá trị lớn nhất, nhỏ nhất của hàm số \(y=\dfrac{x-1}{x^2+1}\) trên đoạn \(D=\left[\dfrac{3}{2};3\right]\) .
- \(\max=\dfrac{-1+\sqrt{2}}{2};\min=\dfrac{171}{865}\)
- \(\max=\dfrac{2}{13};\min=\dfrac{1}{5}\)
- \(\max=\dfrac{-1+\sqrt{2}}{2};\min=\dfrac{2}{13}\)
- \(\max=\dfrac{-1+\sqrt{2}}{2};\min=\dfrac{1}{5}\)
Hướng dẫn giải:
\(y'=\dfrac{-x^2+2x+1}{\left(x^2+1\right)^2}\) có hai nghiệm \(x=1\pm\sqrt{2}.\) Trong khoảng \(\left(\dfrac{3}{2};3\right)\) , đạo hàm chỉ triệt tiêu tại \(x=1+\sqrt{2}.\) So sánh giá trị của hàm số tại \(\dfrac{3}{3};1+\sqrt{2};3\) là \(\dfrac{2}{13},\dfrac{-1+\sqrt{2}}{2},\dfrac{1}{5}\) suy ra \(\max=\dfrac{-1+\sqrt{2}}{2};\min=\dfrac{2}{13}\).
Biết rằng đường thẳng \(y=2x-1\) cắt đồ thị hàm số \(y=\frac{-x-1}{x^2}\) tại 1 điểm duy nhất. Tính tung độ giao điểm ?
- 10
- -2
- \(\sqrt{2}\)
- \(\frac{11}{4}\)
Hướng dẫn giải:
Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y=x^4-2mx^2+2m+m^4\) có ba điểm cực trị là ba đỉnh của một tam giác đều.
- \(m=-1\)
- \(m=2\)
- \(m=\sqrt[3]{3}\)
- \(m=\pm\sqrt[3]{3}\)
Hướng dẫn giải:
\(y'=4x^3-4mx=4x\left(x^2-m\right)\)
Để đồ thị hàm số có ba điểm cực trị, cần và đủ là \(y'\) có ba nghiệm phân biệt, hay là phương trình \(x^2-m=0\) có hai nghiệm phân biệt khác 0, suy ra \(m>0\).
Đảo lại, nếu \(m>0\) thì đồ thị có ba điểm cực trị là \(A\left(0;2m+m^4\right),B_{1,2}\left(\pm\sqrt{m};m^4-m^2+2m\right).\)Tam giác \(AB_1B_2\) cân tại \(A\) có đáy \(B_1B_2=2\sqrt{m},\)cạnh bên \(AB_1=\sqrt{m+m^4}\) nên để tam giác tạo thành là tam giác đều, cần và đủ là \(AB_1=B_1B_2\Leftrightarrow\sqrt{m+m^4}=2\sqrt{m}\Leftrightarrow m^4=3m\Leftrightarrow m=\sqrt[3]{3}.\)
Đồ thị hàm số \(y=\dfrac{m\left|x\right|+1}{\left(m^2+1\right)\sqrt{x^2-1}}\) (với \(m\ne0;m\ne-1\)) có bao nhiêu đường tiệm cận (đứng, ngang) ?
- 3
- 2
- 1
- 0
Hướng dẫn giải:
Hàm số có tập xác định là: \(\left(-\infty;-1\right)\cup\left(1;+\infty\right)\).
- Tiệm cận đứng:
\(\lim\limits_{x\rightarrow-1^-}\dfrac{m\left|x\right|+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\lim\limits_{x\rightarrow-1^-}\dfrac{-mx+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\left\{\begin{matrix}+\infty.m+1>0\\-\infty,m+1< 0\end{matrix}\right.\)
Vậy x = -1 là tiệm cận đứng
\(\lim\limits_{x\rightarrow1^+}\dfrac{m\left|x\right|+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\lim\limits_{x\rightarrow1^+}\dfrac{mx+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\left\{\begin{matrix}+\infty,m+1>0\\-\infty,m+1< 0\end{matrix}\right.\)
Vậy x = 1 là tiệm cận đứng thứ hai
- Tiệm cận ngang:
\(\lim\limits_{x\rightarrow+\infty}\dfrac{m\left|x\right|+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{mx}{x}+\dfrac{1}{x}}{\left(m^2+1\right)\sqrt{1-\dfrac{1}{x^2}}}=\dfrac{m}{m^2+1}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{m\left|x\right|+1}{\left(m^2+1\right)\sqrt{x^2-1}}=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{m\left(-x\right)}{x}+\dfrac{1}{x}}{-\left(m^2+1\right)\sqrt{1-\dfrac{1}{x^2}}}=\dfrac{-m}{-\left(m^2+1\right)}=\dfrac{m}{m^2+1}\)
(chú ý khi x < 0 thì \(x=-\sqrt{x^2}\))
Vậy hàm số có 1 tiệm cận ngang là \(y=\dfrac{m}{m^2+1}\)
Kết luận: Hàm số có 1 tiệm cận ngang và 2 tiệm cận đứng.
Kí hiệu \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x^2\ln x\) trên đọan \(\left[1;e\right]\). Tính hiệu \(M-m\)
- \(e^2-\dfrac{e}{2}\)
- \(e^2-\dfrac{\sqrt{e}}{4}\)
- \(e^2\)
- \(\dfrac{\sqrt{e}}{4}-1\)
Hướng dẫn giải:
\(y'=2x\ln x+x=x\left(2\ln x+1\right)\);
\(y'=0\Leftrightarrow2\ln x+1=0\Leftrightarrow x=e^{-\frac{1}{2}}\notin\left(1;e\right).\)
So sánh hai giá trị \(y\left(1\right)=0,y\left(e\right)=e^2\) ta có \(M=e^2,m=0\Rightarrow M-m=e^2.\)
Tìm các giá trị của tham số m sao cho hàm số \(y=\frac{1}{3}mx^3-\left(m-1\right)x^2+3\left(m+2\right)x+\frac{1}{3}\) đồng biến trên khoảng \(\left(2;+\infty\right)\) ?
- \(m< 0\)
- \(m>0\)
- \(m=0\)
- \(m\ge0\)
Hướng dẫn giải:
Tính tổng các nghiệm của phương trình \(\sqrt{2^x\sqrt[3]{4^x.0,125^{\frac{1}{x}}}}=4\sqrt[3]{2}\) ?
- 2,8
- 5,6
- 4,25
- -1
Hướng dẫn giải:
Tính đạo hàm của hàm số \(y=\left(2x+1\right)^{\frac{1}{3}}\left(3x-1\right)^{\frac{1}{3}}\) ?
- \(\frac{1}{3}\left(2x+1\right)^{-\frac{2}{3}}\left(3x-1\right)^{-\frac{2}{3}}\)
- \(\frac{1}{3}\left(2x+1\right)^{-\frac{2}{3}}\left(3x-1\right)+\frac{1}{3}\left(2x+1\right)\left(3x-1\right)^{-\frac{2}{3}}\)
- \(\frac{12x+1}{3}\left(6x^2+x-1\right)^{-\frac{2}{3}}\)
- \(\frac{1}{3}\left(6x^2+x-1\right)^{-\frac{2}{3}}\)
Hướng dẫn giải:
Sử dụng tính chất tích hai lũy thừa cùng số mũ ta viết lại y như sau:
\(y=\left(2x+1\right)^{\frac{1}{3}}\left(3x-1\right)^{\frac{1}{3}}=\left[\left(2x+1\right)\left(3x-1\right)\right]^{\frac{1}{3}}\)
\(=\left(6x^2+x-1\right)^{\frac{1}{3}}\)
Suy ra:
\(y'=\frac{1}{3}\left(12x+1\right)\left(6x^2+x-1\right)^{-\frac{2}{3}}\)
Tìm tập xác định \(D\) của hàm số \(y=\left(\dfrac{x^2-1}{x+2}\right)^{\sqrt[3]{3}}\) ?
- \(D=\left(-2;-1\right)\cup\left(1;+\infty\right)\)
- \(D=\left(-\infty;-2\right)\cup\left(-1;1\right)\)
- \(D=\left(1;+\infty\right)\)
- \(D=\left(-\infty;-2\right)\)
Hướng dẫn giải:
Vì \(\sqrt[3]{3}\notin\mathbb{Z}\) nên hàm số đã cho sẽ xác định khi và chỉ khi \(\left(\dfrac{x^2-1}{x+2}\right)>0\Leftrightarrow\left(x^2-1\right)\left(x+2\right)>0\Leftrightarrow x\in\)\(\left(-2;-1\right)\cup\left(1;+\infty\right)\). Vậy \(D=\left(-2;-1\right)\cup\left(1;+\infty\right)\).
Giải bất phương trình \(\left(2,5\right)^{x+1}-\left(0,4\right)^x+1,5< 0\)
- x > 1
- x > 2
- x < -1
- x < -2
Hướng dẫn giải:
Viết lại phương trình dạng:
\(\left(\frac{5}{2}\right)^{x+1}-\left(\frac{2}{5}\right)^x+1,5< 0\)
Xét hàm số \(f\left(x\right)=\ln\left(2x-1\right)+\ln\left(1-x\right)\) .Trong các khẳng định sau, khẳng định nào đúng ?
- \(f'\left(\frac{3}{4}\right)=0\)
- \(f'\left(0\right)=3\)
- \(f'\left(2\right)=-\frac{5}{3}\)
- \(f'\left(-1\right)=\frac{7}{6}\)
Hướng dẫn giải:
\(f'\left(x\right)=\frac{2}{2x-1}-\frac{1}{1-x}=\frac{3-4x}{\left(2x-1\right)\left(1-x\right)}\)
Cho \(\log_ab=3;\log_ac=-2\). Hãy tính \(\log_a\left(a^3b^2\sqrt{c}\right)\) ?
- 5
- 8
- -8
- 4
Hướng dẫn giải:
Tính đạo hàm của hàm số \(y=\left(x^2-x+1\right)4^x\) ?
- \(y'=\left(2x-1\right)4^x.ln4\)
- \(y'=\left(2x-1\right)4^x+\left(x^2-x+1\right)4^x\)
- \(y'=\left(2x-1\right)4^x+\left(x^2-x+1\right).4^x.ln4\)
- \(y'=\left(2x-1\right)2^x+\left(x^2-x+1\right).2^{x^2}.ln4\)
Hướng dẫn giải:
Cho a, b là hai số dương khác 1. Trong các khẳng định sau, khẳng định nào đúng ?
- \(ba^{\frac{2}{\log_ba}+1}-2a^{\log_ab+1}b^{\log_ba+1}+ab^{\frac{2}{\log_ab}+1}=ab\left(a-b\right)^2\)
- \(ba^{\frac{2}{\log_ba}+1}-2a^{\log_ab+1}b^{\log_ba+1}+ab^{\frac{2}{\log_ab}+1}=ab\left(a+b\right)^2\)
- \(ba^{\frac{2}{\log_ba}+1}-2a^{\log_ab+1}b^{\log_ba+1}+ab^{\frac{2}{\log_ab}+1}=ab\left(\frac{1}{a}-\frac{1}{b}\right)^2\)
- \(ba^{\frac{2}{\log_ba}+1}-2a^{\log_ab+1}b^{\log_ba+1}+ab^{\frac{2}{\log_ab}+1}=\frac{\left(a-b\right)^2}{ab}\)
Hướng dẫn giải:
Có:
\(ba^{\frac{2}{\log_ba}+1}=b.a^{2\log_ab+1}=b.\left(a^{2\log_ab}\right)a=b.a^{\log_ab^2}.a=b.b^2.a=b^3a\)
\(a^{\log_ab+1}b^{\log_ba+1}=b.a.a.b=a^2b^2\)
\(ab^{\frac{2}{\log_ab}+1}=ab^{2\log_ba}.b=a.a^2.b=a^3b\)
Vậy:
\(ba^{\frac{2}{\log_ba}+1}-2a^{\log_ab+1}b^{\log_ba+1}+ab^{\frac{2}{\log_ab}+1}=b^3a+2a^2b^2+a^3b\)
\(=ab\left(b^2+2ab+a^2\right)=ab\left(a+b\right)^2\)
Xét bất phương trình \(\log_{\frac{2x-1}{x}}5< \log_{\frac{2x-1}{x}}2\) (*)
Trong các khẳng định sau, khẳng định nào đúng ?
- (*) \(\Leftrightarrow\frac{1}{\log_{\frac{2x-1}{x}}5}>\frac{1}{\log_{\frac{2x-1}{x}}2}\)
- (*) \(\Leftrightarrow\log_2\frac{2x-1}{x}< \log_5\frac{2x-1}{x}\)
- (*) \(\Leftrightarrow\left\{\begin{matrix}\left\{\begin{matrix}\frac{2x-1}{x}>1\\5< 2\end{matrix}\right.\\\left\{\begin{matrix}\frac{2x-1}{x}< 1\\5>2\end{matrix}\right.\end{matrix}\right.\)
- (*) \(\Leftrightarrow0< \frac{2x-1}{x}< 1\)
Hướng dẫn giải:
Tìm tất cả các giá trị của tham số m để phương trình \(\log\left(mx\right)=2\log\left(x+1\right)\) có hai nghiệm phân biệt ?
- \(m>4\)
- \(m\ge4\)
- \(m=-1\)
- \(m< 0;m\ge4\)
Hướng dẫn giải:
\(\log\left(mx\right)=2\log\left(x+1\right)\)
\(\Leftrightarrow\log\left(mx\right)=\log\left(x+1\right)^2\)
\(\Leftrightarrow\left\{\begin{matrix}mx>0\\x+1>0\\mx=\left(x+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}x+1>0\\mx=\left(x+1\right)^2\end{matrix}\right.\)
(điều kiện mx > 0 nghiễm nhiên tỏa mãn nếu 2 điều kiện trên thỏa mãn)
\(\Leftrightarrow\left\{\begin{matrix}x>-1\\m=\frac{\left(x+1\right)^2}{x}\end{matrix}\right.\)
Trong các khẳng định sau, khẳng định nào sai ?
- \(\int\frac{1}{2x}dx=\ln\left|2x\right|+C\)
- \(\int e^xdx=e^x+C\)
- \(\int\sin xdx=-\cos x+C\)
- \(\int4^xdx=\frac{4^x}{\ln4}+C\)
Hướng dẫn giải:
\(\int\frac{1}{2x}dx=\frac{1}{2}\ln\left|2x\right|+C\)
Tìm hàm số \(f\left(x\right)\) biết rằng đồ thị hàm số \(y=f\left(x\right)\) cắt trục tung tại điểm có tung độ bằng e và có \(f'\left(x\right)=3x^2+2x+1,\forall x\) ?
- \(f\left(x\right)=\cos2x+e-1\)
- \(f\left(x\right)=x^3+x^2+x+e\)
- \(f\left(x\right)=x^3+x^2+x+1\)
- \(f\left(x\right)=x^3+x^2+e\)
Hướng dẫn giải:
\(f\left(x\right)=\int f'\left(x\right)\text{dx}=\int\left(3x^2+2x+1\right)\text{dx}=x^3+x^2+x+C\)
\(f\left(0\right)=e\) nên suy ra \(C=e\)
Vậy \(f\left(x\right)=x^3+x^2+x+e\)
Biết \(\delta\left(t\right)=3\left(25t+1\right)^2\) là tốc độ tăng dân số của một huyện tại năm thứ t tính từ thời điểm \(t=0\) (thời điểm hoàn thành thống kê dân số: ngày mùng 1 tháng 1 năm 2000), trong đó \(t\) được tính bằng năm, \(\delta\left(t\right)\) được tính bằng người / năm. Hãy tính xem trong khoảng thời gian từ ngày mùng 1 tháng 1 năm 2001 đến ngày mùng 1 tháng 1 năm 2004, số dân huyện đó tăng thêm bao nhiêu người?
- 41.212
- 412.120
- 17.559
- 175.590
Hướng dẫn giải:
Sau 4 năm, số dân tăng là :
Đặt \(I=\int_1^2\frac{dx}{x\sqrt{1+x^2}}\) và \(t=\sqrt{1+x^3}\).
Trong các khẳng định sau, khẳng định nào sai ?
- \(x^3=t^2-1\)
- \(x^2dx=\frac{2}{3}tdt\)
- \(I=\int\limits^2_1\frac{2}{3\left(t^2+1\right)}dt\)
- \(I=\frac{1}{3}\int\limits^3_{\sqrt{2}}\left(\frac{1}{t-1}-\frac{1}{t+1}\right)dt\)
Tính tích phân \(I=\int\limits^1_0\left(x-1\right)e^xdx\) ?
- \(I=10,223\)
- \(I=e+\frac{1}{2}\)
- \(I=2-e^2\)
- \(I=2-e\)
Hướng dẫn giải:
Tính diện tích hình phẳng giới hạn bởi các đường \(x=\sqrt{y};x+y-2=0;y=0\) ?
- \(\frac{5}{6}\)
- \(\frac{6}{5}\)
- \(\frac{5}{7}\)
- \(\frac{7}{5}\)
Hướng dẫn giải:
Khử x từ 2 phương trình đầu ta được \(\sqrt{y}=2-y\). Phương trình này có nghiệm duy nhất y = 1.
Hình phẳng đã cho được giới hạn bởi:
\(x=\sqrt{y};x=2-y;y=0;y=1\)
Diện tích là:
S = \(\left|\int\limits^1_0\left(2-y-\sqrt{y}\right)\text{dy}\right|\)
\(=\left|\int\limits^1_0\left(2-y-y^{\frac{1}{2}}\right)\text{dy}\right|=\frac{5}{6}\)
Tính thể tích khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi các đường \(x=\frac{\pi}{2};x=\pi;y=0;y=\sqrt{1+\cos^4x+\sin^4x}\) ?
- \(\frac{7}{8}\pi\)
- \(\frac{7}{8}\pi^2\)
- \(\frac{7}{8}\pi^3\)
- \(\frac{5}{8}\pi^2\)
Hướng dẫn giải:
\(V=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left[\left(\sqrt{1+\cos^4x+\sin^4x}\right)^2-0^2\right]\text{dx}\)
\(=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left(1+\cos^4x+\sin^4x\right)\text{dx}\)
\(=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left[1+\left(\cos^2x+\sin^2x\right)^2-2\cos^2x\sin^2x\right]\text{dx}\)
\(=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left[1+1^2-\frac{1}{2}\sin^22x\right]\text{dx}\)
\(=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left[2-\frac{1}{2}\frac{1-\cos4x}{2}\right]\)
\(=\pi\int\limits^{\pi}_{\frac{\pi}{2}}\left(\frac{7}{4}+\frac{1}{4}\cos4x\right)\text{dx}\)
\(=\pi\left(\frac{7}{4}+\frac{1}{16}\sin4x\right)|^{\pi}_{\frac{\pi}{2}}\)
\(=\frac{7\pi^2}{8}\)
Trong các khẳng định sau, khẳng định nào sai ?
- Số phức \(z=\pi-5\ln2\) có phần thực là \(\pi\)
- Có vô số phức bằng số phức liên hợp của nó
- Số phức \(z=3\sqrt{2}-i\) có phần ảo là \(-1\)
- Nếu số phức \(z\) là số thực thì giá trị tuyệt đối của \(z\) cũng là môđun của \(z\)
Hướng dẫn giải:
\(z=\pi-5\ln2=\left(\pi-5\ln2\right)+0i\) có phần thực là \(\pi-5\ln2\) (chứ không phải là \(\pi\)).
Cho hai số phức \(z_1=1-5i;z_2=3+2i\). Tính phần ảo của số phức \(v=\frac{z_1^2}{z_2}\) ?
- \(\sqrt{19}\)
- \(\frac{18}{13}i\)
- \(\frac{18}{13}\)
- \(\frac{13}{18}\)
Hướng dẫn giải:
\(z_1^2=\left(1-5i\right)^2=1-10i+25i^2=1-10i-25=-24-10i\)
\(v=\frac{z_1^2}{z_2}=\frac{-24-10i}{3+2i}=\frac{\left(-24-10i\right)\left(3-2i\right)}{\left(3+2i\right)\left(3-2i\right)}=\frac{-92+18i}{3^2-4i^2}=\frac{-92+18i}{13}\)
Phần ảo của \(v\) là \(\frac{18}{13}\)
Khi số phức \(z\) thay đổi tùy ý, tập hợp các điểm biểu diễn số phức \(v=z^2+\left(\overline{z}\right)^2\) là đường nào trong mặt phẳng phức ?
- Trục tung
- Đường phân giác góc phần tư (I), (III)
- Trục hoành
- Đường phân giác góc phần tư (I), (III) và đường phân giác góc phần tư (I), (IV)
Hướng dẫn giải:
Với \(z=x+yi\) thì
\(v=z^2+\left(\overline{z}\right)^2=\left(x+yi\right)^2+\left(x-yi\right)^2=2\left(x^2+y^2i^2\right)=2\left(x^2-y^2\right)\in\mathbb{R}\)
Do đó các điểm biểu diễn \(v=z^2+\left(\overline{z}\right)^2\) nằm trên trục hoành.
Kí hiệu \(i\) là đơn vị ảo. Tìm tất cả các cặp số phức \(v,z\) thỏa mãn hệ phương trình \(\left\{\begin{matrix}iv-3z=i+1\\2v-iz=i-2\end{matrix}\right.\)
- \(v=3-4i;z=2+5i\)
- \(v=-\frac{5}{7}+\frac{2}{7}i;z=-\frac{3}{7}-\frac{4}{7}i\)
- \(v=-\frac{3}{7}-\frac{4}{7}i;z=-\frac{5}{7}+\frac{2}{7}i\)
- \(v=-1+\frac{2}{5}i;z=-\frac{3}{5}-\frac{4}{5}i\)
Hướng dẫn giải:
Từ phương trình thứ hai, tính \(v\) theo \(z\) rồi thế vào phương trình đầu ta được một phương trình bậc nhất một ẩn \(z\) từ đó tính được \(z=-\frac{3}{7}-\frac{4}{7}i\), thế vào biểu thức tính \(v\) theo \(z\) ta tính được \(v=-\frac{5}{7}+\frac{2}{7}i.\) Hệ có nghiệm duy nhất là \(v=-\frac{5}{7}+\frac{2}{7}i;z=-\frac{3}{7}-\frac{4}{7}i\).
Cách khác: Có thể giải hệ đã cho bằng định thức cấp 2 hoặc dùng máy tính cầm tay (MODE 2) để kiểm tra đáp số nào trong 4 đáp số đã nêu là đúng)
Kí hiệu \(i\) là đơn vị ảo. Trong các khẳng định sau, khẳng định nào sai ?
- \(i+i^2+i^3+...+i^{2000}=0\)
- \(i+i^2+i^3+...+i^{999}=-1\)
- \(i+i^2+i^3+...+i^{2007}=-i\)
- \(1+i+i^2+i^3+...+i^{1000}=1\)
Hướng dẫn giải:
Có \(i+i^2+i^3+i^4=\left(1+i^2\right)\left(i+i^2\right)=0.\left(i+i^2\right)=0\Rightarrow i+i^2+i^3+...+i^k=0,\forall k⋮4.\) Do đó
a) \(2000⋮4\Rightarrow i+i^2+i^3+...+i^{2000}=0.\)
b) \(1000⋮4\Rightarrow i+i^2+...+i^{1000}=0\Rightarrow i+i^2+...+i^{999}=-i^{1000}=-\left(\left(i^2\right)\right)^{500}=-\left(-1\right)^{500}=-1\)
c) \(2008⋮4\Rightarrow i+i^2+...+i^{2008}=0\Rightarrow i+i^2+...+i^{2007}=-i^{2008}=-\left(\left(i^2\right)^{1004}\right)=-\left(-1\right)^{2004}=-1\) nên khẳng định \(i+i^2+i^3+...+i^{2007}=-i\) là khẳng định sai.
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức \(z\) thỏa mãn điều kiện : Số phức \(v=\left(z-i\right)\left(2+i\right)\) một số thuần ảo.
- Đường tròn \(x^2+y^2=2\)
- Đường thẳng \(x+2y-2=0\)
- Đường thẳng \(2x-y+1=0\)
- Đường parabol \(2x=y^2\)
Hướng dẫn giải:
Số phức \(z=x+yi,\left(x,y\in\mathbb{R}\right)\) được biểu diễn bởi điểm \(M\left(x;y\right)\). Ta có
\(v=\left(z-i\right)\left(2+i\right)=\left(x+\left(y-1\right)i\right)\left(2+i\right)=\left(2x-y+1\right)+\left(x+2y-2\right)i\)
\(v\) là số thuần ảo khi và chỉ khi \(2x-y+1=0\Leftrightarrow M\left(x;y\right)\in\) đường thẳng \(2x-y+1=0\).
Cho hình chóp tứ giác đều S.ABCD có các mặt bên nghiêng với đáy một góc \(45^o\). Gọi M, N, P lần lượt là trung điểm các cạnh bên SA, SB, SD của hình chóp. Tính cạnh đáy của hình chóp đã cho biết khối tứ diện AMNP có thể tích bằng \(18cm^3\) ?
- 12 cm
- 6 cm
- 8 cm
- 16 cm
Hướng dẫn giải:
Gọi M, N là trung điểm các cạnh A'B' và B'C' của khối hộp ABCD.A'B'C'D'. Tính thể tích của khối hộp nếu biết khối tứ diện BD'MN có thể tích \(8cm^3\) ?
- \(48cm^3\)
- \(64cm^3\)
- \(80cm^3\)
- \(40cm^3\)
Hướng dẫn giải:
Tính thể tích khối hộp ABCD.A'B'C'D' biết khối chóp A.BB'D'D có thể tích bằng \(5cm^3\) ?
- \(15cm^3\)
- \(10cm^3\)
- \(40cm^3\)
- \(25cm^3\)
Hướng dẫn giải:
Gọi M. N là trung điểm hai cạnh bên AA', BB' của khối lăng trụ tam giác ABC.A'B'C'. Tính thể tích của khối lăng trụ nếu biết khối đa diện ABCMN có thể tích bằng \(1cm^3\) ?
- \(2cm^3\)
- \(4cm^3\)
- \(6cm^3\)
- \(3cm^3\)
Hướng dẫn giải:
Tính thể tích khối trụ tròn ngoại tiếp khối lăng trụ lục giác đều có cạnh đáy bằng a và diện tích xung quanh bằng \(12a^2\) ?
- \(6\pi a^3\)
- \(\pi a^3\)
- \(2\pi a^3\)
- \(3\pi a^3\)
Hướng dẫn giải:
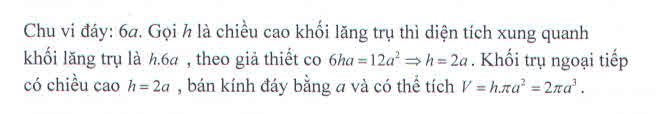
Cho khối lăng trụ có chiều cao đường kính đáy. Kẻ hai bán kính đáy OA và O'B' không song song với nhau rồi cắt khối trụ bởi một mặt phẳng qua A', B' và song song với trục của khối trụ ta được thiết diện có diện tích bằng một nửa diện tích thiết diện phẳng qua trục. Tính góc tạo thành bởi OA, O'B' ?
- \(60^o\)
- \(45^o\)
- \(90^o\)
- \(30^o\)
Hướng dẫn giải:
Cho một khối lập phương và khối trụ với hai đáy là hai đường tròn nội tiếp hai mặt của khối lập phương. Tính thể tích khối lập phương nếu biết khối trụ có diện tích xung quanh là \(25\pi\) ?
- \(27cm^3\)
- \(8cm^3\)
- \(125cm^3\)
- \(5\sqrt{5}cm^3\)
Hướng dẫn giải:
Trong mặt phẳng đã cho tam giác đều ABC tâm O. Khi quay mặt phẳng quanh đường thẳng AO thì tam giác ABC sinh ra một khối nón, đồng thời đường tròn nội tiếp và đường tròn ngoại tiếp ABC thì sinh ra hai khối cầu: một khối cầu tiếp xúc với mặt đáy của khối nón, khối cầu kia chứa đỉnh và đường tròn đáy của khối nón (hai khối cầu này cũng được gọi là khối cầu nội tiếp và khối cầu ngoại tiếp khối nón). Nếu khối cầu nhỏ thể tích \(1cm^3\) thì khối cầu lớn có thể tích bao nhiêu ?
- \(8cm^3\)
- \(27cm^3\)
- \(5cm^3\)
- \(3cm^3\)
Hướng dẫn giải:
Cho bốn điểm \(A\left(1;2;1\right);B\left(2;2;0\right);C\left(3;2;1\right);D\left(1;6;1\right)\). Tìm tọa độ tâm mặt cầu ngoại tiếp tứ diện ABCD ?
- (1; 2; 1)
- (2; 4; 1)
- (1; 4; 2)
- ( 1; 1; 0)
Hướng dẫn giải:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left(P\right):4x+y-2=0\). Đường thẳng nào trong các đường thẳng sau vuông góc với mặt phẳng (P) ?
- \(d:\frac{x-1}{1}=\frac{y+1}{-1}=\frac{z-2}{2}\)
- \(d:\frac{x-3}{4}=\frac{y-1}{1}=\frac{z}{2}\)
- \(d:\frac{x-4}{1}=\frac{y-1}{1}=\frac{z-0}{1}\)
- \(\left\{\begin{matrix}x=4t\\y=t\\z=0\end{matrix}\right.\)
Hướng dẫn giải:
Chỉ có đường thẳng \(\left\{\begin{matrix}x=4t\\y=t\\z=0\end{matrix}\right.\) có vecto chỉ phương (4;1;0) song song với vecto pháp tuyến của (P)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left(P\right):3x-4z-1=0\). Mặt cầu nào trong các mặt cầu sau đây không cắt (P) ?
- \(\left(x-1\right)^2+\left(x-3\right)^2+z^2=1\)
- \(\left(x-1\right)^2+\left(y-3\right)^2+z^2=\frac{4}{25}\)
- \(\left(x-1\right)^2+\left(y-3\right)^2+z^2=\frac{1}{25}\)
- \(\left(x-1\right)^2+\left(y-3\right)^2+z^2=5\)
Hướng dẫn giải:
Cả 4 mặt cầu đều có tâm là I(1;3;0) và khoảng cách từ I đến (P) là:
\(d=\frac{3.1-4.0-1}{\sqrt{3^2+\left(-4\right)^2}}=\frac{2}{5}\)
\(\Rightarrow d^2=\frac{4}{25}\)
Chỉ có mặt cầu \(\left(x-1\right)^2+\left(y-3\right)^2+z^2=\frac{1}{25}\) có bán kính nhỏ hơn khoảng cách từ tâm I đến (P) nên mặt cầu này không cắt (P).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left(1;2;-4\right);B\left(5;4;2\right)\). Viết phương trình mặt phẳng trung trực của đoạn AB ?
- \(4x+2y+6z-11=0\)
- \(2x+3z-3=0\)
- \(10x+9y+5z-70=0\)
- \(2x+y+3z-6=0\)
Hướng dẫn giải:
Gọi M(x;y;z) thuộc (P) thì khoảng cách AM = BM.
Suy ra:
\(\sqrt{\left(x-1\right)^2+\left(y-2\right)^2+\left(z+4\right)^2}=\sqrt{\left(x-5\right)^2+\left(y-4\right)^2+\left(z-2\right)^2}\)
\(\Leftrightarrow8x+4y+12z-24=0\)
\(\Leftrightarrow2x+y+3z-6=0\)
Viết phương trình mặt phẳng (P) qua điểm \(M\left(1;-1;1\right)\) và chứa trục Oy ?
- \(x+z=0\)
- \(x-z=0\)
- \(x-y=0\)
- \(x+y=0\)
Hướng dẫn giải:
Trong không gian tọa độ Oxyz, gọi A, B, C lần lượt là hình chiếu vuông góc của điểm \(M\left(8;-2;4\right)\) lên các trục Ox, Oy, Oz. Viết phương trình mặt phẳng đi qua A, B, C ?
- \(x+4y+2z-8=0\)
- \(x+4y-2z-8=0\)
- \(x-4y-2z-8=0\)
- \(x-4y+2z-8=0\)
Hướng dẫn giải:
Cho hai mặt phẳng \(\left(P\right):x+2y+2z+3=0;\left(Q\right):x+2y+2z+7=0\) và đường thẳng \(d:\left\{\begin{matrix}x=t\\y=-1\\z=-t\end{matrix}\right.\). Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d và tiếp xúc với hai mặt phẳng đã cho :
- \(\left(x+3\right)^2+\left(y+1\right)^2+\left(z-3\right)^2=\frac{4}{9}\)
- \(\left(x+3\right)^2+\left(y-1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
- \(\left(x+3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
- \(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
Hướng dẫn giải:
Tìm các giá trị của tham số m để đường thẳng xác định bởi \(\left\{\begin{matrix}2x+3y-2=0\\my+2z+4=0\end{matrix}\right.\) nằm trong mặt phẳng \(\left(P\right):2x-y-2z-6=0\)
- \(m=4\)
- \(m=-4\)
- \(m=2\)
- \(m=-2\)
Hướng dẫn giải:
00:00:00