Cảnh báo
Bạn cần đăng nhập mới làm được đề thi này
Cho hàm số \(y=f\left(x\right)\) với tập xác đinh D=[a;c] có đồ thị :
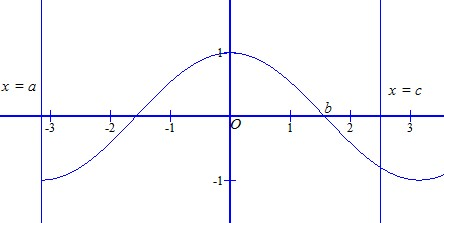
Trong các khẳng định sau, khẳng định nào sai ?
Cho hàm số \(y=f\left(x\right)\), liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau :

Đường nào trong các đường sau đây có thể là đồ thị của hàm số đã cho ?
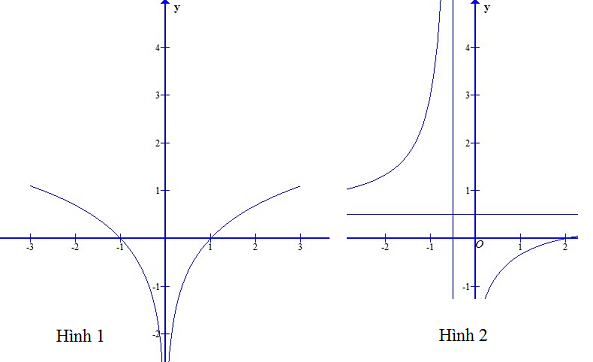
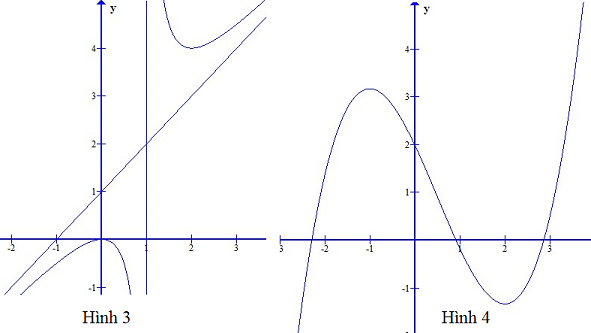
Từ bảng biến thiên ta thấy tập xác định của hàm số là \(\left(-\infty;+\infty\right)\) nên đồ thị hàm số không có tiệm cận đứng. Chỉ có Hình 4 là đồ thị không có tiệm cận đứng.
Trong các khoảng sau đây, hãy chọn một khoảng mà hàm số \(y=\ln x^2\) đồng biến trong khoảng đó ?

Trong các đường cong cho sau đây, đường nào là đồ thị của hàm \(y=\frac{x^4}{4}-2x^2+6\)

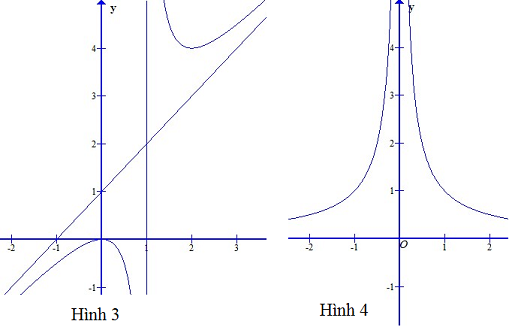
Tập xác định của hàm số là \(\left(-\infty;+\infty\right)\) nên đồ thị sẽ không có tiệm cận đứng. Trong các đồ thị đã cho chỉ có đồ thị trong Hình 1 là không có tiệm cận đứng.
Tìm các điểm cực tiểu của hàm số \(y=\sin2x-x\) ?

Tìm giá trị lớn nhất, bé nhất của hàm số \(y=\dfrac{x^2+1}{x-1}\) trên tập \(D=\left[\dfrac{3}{2};3\right]\).
Trong khoảng \(\left(\dfrac{3}{2};3\right)\) đạo hàm \(y'=\dfrac{x^2-2x-1}{\left(x-1\right)^2}\) chỉ có 1 nghiệm \(x=1+\sqrt{2}.\) Ta có
\(y\left(\dfrac{3}{2}\right)=\dfrac{13}{2},y\left(1+\sqrt{2}\right)=2+2\sqrt{2},y\left(3\right)=5.\)
Từ đó GTLN\(=\dfrac{13}{2},\)GTNN\(=2+2\sqrt{2}.\)
Biết rằng đồ thị hàm số \(y=\left(x+1\right)^3\) và đồ thị hàm số \(y=-x^3+2x^2+2x+2\) cắt nhau tại một điểm duy nhất. Tính tung độ \(y_0\) của giao điểm đó ?

Tìm các giá trị của tham số m để đồ thị hàm số \(y=x^3+3x^2+m\) có hai điểm cực trị A, B sao cho gốc tọa độ O cùng với A và B là 3 đỉnh một tam giác vuông tại O?
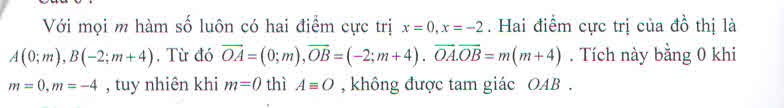
Đồ thị hàm số \(y=\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}\) có bao nhiêu đường tiệm cận (đứng, ngang) ?
Vì mẫu thức \(\left(m^2+1\right)\sqrt{x^2-4}\) có 2 nghiệm \(x=\pm2\) không phải là nghiệm của tử thức nên \(\lim\limits_{x\rightarrow\pm2}y=\infty\Rightarrow x=\pm2\) là 2 tiệm cận đứng.
Vì \(y=\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{\dfrac{x}{\left|x\right|}+\dfrac{1}{\left|x\right|}}{\left(m^2+1\right)\sqrt{1=\dfrac{4}{x^2}}}\) nên \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{1+\dfrac{1}{x}}{\left(m^2+1\right)\sqrt{1-\dfrac{4}{x^2}}}=\dfrac{1}{m^2+1}\) và
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{-1-\dfrac{1}{x}}{\left(m^2+1\right)\sqrt{1-\dfrac{4}{x^2}}}=\dfrac{-1}{m^2+1}\), do đó \(y=\dfrac{1}{m^2+1}\) là tiệm cận ngang (bên phải) và \(y=-\dfrac{1}{m^2+1}\) là tiệm cận ngang (bên trái).
Kí hiệu\(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\cos^4x+\sin^2x-2\). Tính tích \(Mm.\)
Đặt \(t=\cos^2x,t\in\left[0;1\right]\) thì \(y=t^2-t-1.\) Hàm số \(f\left(t\right)=t^2-t-1\) có \(f'\left(t\right)=2t-1\) triệt tiêu tại \(t=\dfrac{1}{2}\in\left(0;1\right)\). So sánh \(f\left(0\right)=-1,f\left(\dfrac{1}{2}\right)=-\dfrac{5}{4},f\left(1\right)=-1\) suy ra \(M=-1,m=-\dfrac{5}{4}\Rightarrow Mm=\dfrac{5}{4}.\)
Tìm các giá trị của tham số \(m\) sao cho đồ thị hàm số \(y=x^3-3mx^2+4m^3\) có hai điểm cực trị đối xứng nhau qua đường thẳng \(y=x\) .
Để hàm số có hai điểm cực trị, cần và đủ là \(y'=3x^2-6mx=3x\left(x-2m\right)\) phải có hai nghiệm khác nhau, tức là \(m\ne0\).
Khi đó, \(y'\) có hai nghiệm là \(0\) và \(2m\) và hai điểm cực trị là: \(A\left(0;4m^3\right),B\left(2m;0\right)\). Hai điểm này sẽ đối xứng nhau qua đường thằng \(y=x\) khi và chỉ khi \(4m^3=2m\Leftrightarrow m=\pm\dfrac{1}{\sqrt{2}}\) (do điều kiện \(m\ne0\)).
Tính tổng các nghiệm của phương trình \(0,6^x\left(\frac{25}{9}\right)^{x^2-12}=\left(\frac{27}{125}\right)^3\)
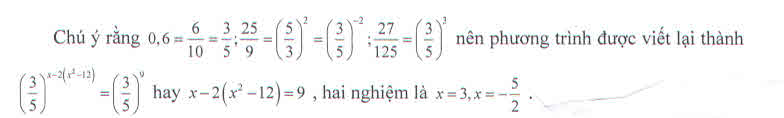
Tính đạo hàm của hàm số \(y=\left(\frac{2x-1}{x+1}\right)^{\sqrt{2}}\)
Sử dụng \(\left(u^{\alpha}\right)'=\alpha u^{\alpha-1}u'\) và \(\left(\frac{u}{v}\right)'=\frac{v.u'-u.v'}{v^2}\)
\(y'=\sqrt{2}.\frac{\left(x+1\right).2-\left(2x-1\right).1}{\left(x+1\right)^2}.\left(\frac{2x-1}{x+1}\right)^{\sqrt{2}-1}\)
\(=\sqrt{2}.\frac{3}{\left(x+1\right)^2}.\left(\frac{2x-1}{x+1}\right)^{\sqrt{2}-1}\)
\(=\frac{3\sqrt{2}}{\left(x+1\right)^2}.\left(\frac{2x-1}{x+1}\right)^{\sqrt{2}-1}\)
Tìm tập xác định D của hàm số \(y=\left(\frac{x-2}{x+1}\right)^{-3}\)
Đầu tiên để hàm số có nghĩa thì mẫu số \(x+1\ne0\Leftrightarrow x\ne-1\)
Theo định nghĩa lúy thừa số mũ âm ta có:
\(y=\left(\frac{x-2}{x+1}\right)^{-3}=\frac{1}{\left(\frac{x-2}{x+1}\right)^3}=\left(\frac{x+1}{x-2}\right)^3\)
Ta cần thêm điều kiện \(x\ne2\).
Vậy điều kiện là:
\(x\ne-1;x\ne2\)
Giải bất phương trình \(2^{2x-1}+2^{2x-2}+2^{2x-3}\ge448\) ?
Viết lại bất phương trình thành
\(2^{2x-3}\left(2^2+2+1\right)\ge448\)
\(\Leftrightarrow2^{2x-3}.7\ge448\)
\(\Leftrightarrow2^{2x-3}\ge64\)
\(\Leftrightarrow2^{2x-3}\ge2^6\)
\(\Leftrightarrow2x-3\ge6\)
\(\Leftrightarrow x\ge\frac{9}{2}\)
Xét hàm số \(f\left(x\right)=\ln\sqrt{x^2-x-12}\).
Trong các khẳng định sau, khẳng định nào sai ?

Cho \(\log_ab=3;\log_ac=-2\). Hãy tính \(\log_a\frac{a^4\sqrt[3]{b}}{c^3}\)
\(\log_a\frac{a^4\sqrt[3]{b}}{c^3}=4\log_aa+\frac{1}{3}\log_ab-3\log_ac\)
\(=4.1+\frac{1}{3}.3-3.\left(-2\right)=11\)
Tính đạo hàm \(y=\frac{x^2+x}{9^x}\) ?

Cường độ động đất M được cho bởi công thức \(M=\lg A-\lg A_0\), với A là biên độ rung chấn tối đa và \(A_0\) là một biên độ chuẩn (hằng số). Đầu thế kỉ 20, một trận động đất ở San Francisco có cường độ 8,3 độ Richter. Trong cùng năm đó, một trận động đất khác ở Nam Đại Tây Dương có cường độ 7,3 độ Richter. Hỏi trận động đất ở San Francisco có biên độ gấp bao nhiêu lần biên độ của trận động đất ở Nam Đại Tây Dương ?

Xét phương trình \(\ln^2\left(-x\right)-3\ln\left(x^2\right)+9=0\) (*). Trong các khẳng định sau, khẳng định nào đúng ?
Điều kiện: \(-x>0\Leftrightarrow x< 0\)
\(\ln^2\left(-x\right)-3\ln\left(x^2\right)+9=0\)
\(\Leftrightarrow\ln^2\left(-x\right)-3\ln\left[\left(-x\right)^2\right]+9=0\)
\(\Leftrightarrow\ln^2\left(-x\right)-6\ln\left(-x\right)+9=0\)
Tìm tất cả các giá trị của tham số m để phương trình \(\log\left(mx\right)=2\log\left(x+1\right)\) có nghiệm ?
Phương trình tương đương:
\(\left\{\begin{matrix}mx>0\\x+1>0\\\log\left(mx\right)=2\log\left(x+1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}mx>0\\x+1>0\\mx=\left(x+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}x+1>0\\mx=\left(x+1\right)^2\end{matrix}\right.\) (vì với 2 điều kiện này đã đảm bảo mx > 0 rồi)
\(\Leftrightarrow\left\{\begin{matrix}x+1>0\\m=\frac{\left(x+1\right)^2}{x}\end{matrix}\right.\)
Vậy m phải là một giá trị của hàm số \(f\left(x\right)=\frac{\left(x+1\right)^2}{x}\) khi \(x>-1\).
\(f'\left(x\right)=\frac{x^2-1}{x^2}\)
Ta thấy \(f'\left(x\right)\) chỉ có 1 nghiệm x=1 trong \(\left(-1;+\infty\right)\).
Ta có bảng biến thiên của f(x) với x > -1:
Nhìn vào bảng biến thiên ta có miền giá trị của f(x) là (\(-\infty;0\)) \(\cup\)[\(4;+\infty\))
Vậy \(m< 0;m\ge4\)
Trong các khẳng định sau, khẳng định nào sai ?
\(\int\cos2xdx=\frac{1}{2}\sin2x+C\)
Cho hàm số \(f\left(x\right)\) thỏa mãn các điều kiện \(f'\left(x\right)=2+\cos2x\) và \(f\left(\frac{\pi}{2}\right)=2\pi\). Trong các khẳng định sau, khẳng định nào sai ?
\(f\left(x\right)=2x+\frac{1}{2}\sin2x+C\)
\(f\left(\frac{\pi}{2}\right)=\pi+C=2\pi\Rightarrow C=\pi\)
Vậy \(f\left(x\right)=2x+\frac{1}{2}\sin2x+\pi\)
Đường ống dẫn nước Sông Đà bị vỡ, lượng nước sạch bị thất thoát với tốc độ tính bằng lít/phút. Tại phút thứ t là \(\mu\left(t\right)=\left(t+1\right)^2\). Tính khối lượng nước sạch thất thoát sau 2 giờ đầu tiên ?

Đặt \(I=\int\limits^{\sqrt{2}}_{\frac{2}{\sqrt{3}}}\frac{dx}{x\sqrt{x^2-1}}\) và \(t=\sqrt{x^2-1}\)
Trong các khẳng định sau, khẳng định nào sai ?

Tính tích phân \(I=\int\limits^2_1\frac{ln\left(1+x\right)}{x^2}dx\) ?
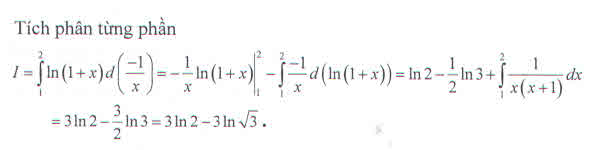
Tính diện tích hình phẳng giới hạn bởi các đường \(y=0;y=3;y=x;y^2=2x\) ?
Hình phẳng đã cho được giới hạn bởi hai đồ thị \(x=y;x=\dfrac{y^2}{2}\) và hai đường thẳng \(y=0,y=3\) nên áp dụng công thức tính diện tích (công thức (3) trang 114), ta được diện tích \(S\) cần tính là \(S=\int^3_0\left|\dfrac{y^2}{2}-y\right|\text{d}y\). Bấm máy tính ta tính được \(S=1,333333333=\dfrac{4}{3}.\)
Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y=\frac{x^3}{3};y=x^2\) ?
Hai đường \(y=\frac{x^3}{3};y=x^2\) cắt nhau tại các điểm có hoành độ là nghiệm của phương trình:
\(\frac{x^3}{3}=x^2\Leftrightarrow x^2\left(x-3\right)=0\Leftrightarrow\left[\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy, thể tích khối tròn xoay tạo thành là:
\(V=\left|\pi\int\limits^3_0\left[\left(\frac{x^3}{3}\right)^2-\left(x^2\right)^2\right]\text{dx}\right|\)
\(=\left|\pi\int\limits^3_0\left(\frac{x^6}{9}-x^4\right)\text{dx}\right|\)
\(=\pi.\left[\frac{x^7}{63}-\frac{x^5}{5}\right]|^3_0=\frac{486\pi}{35}\)
Kí hiệu M là điểm biểu diễn số phức z. M' là điểm biểu diễn số phức \(\overline{z}\). Trong các khẳng định sau, khẳng định nào đúng ?
\(z=x+yi\Rightarrow z'=x-yi\)
Điểm M(x; y) biểu diễn số z và M'(x;-y) là biểu diễn z'. Hai điểm này đối xứng nhau qua trục hoành.
Cho hai số phức \(z_1=\sqrt{3}-2i;z_2=1+\sqrt{3}i\)
Tính số phức liên hợp của \(v=z_1\overline{z_2}-\overline{z_1}.z_2\) ?
\(v=z_1\overline{z_2}-\overline{z_1}.z_2\)
\(=\left(\sqrt{3}-2i\right)\left(1-\sqrt{3}i\right)-\left(\sqrt{3}+2i\right)\left(1+\sqrt{3}i\right)\)
\(=\sqrt{3}-3i-2i+2\sqrt{3}i^2-\sqrt{3}-3i-2i-2\sqrt{3}i^2\)
\(=-10i\)
Khi số phức z thay đổi tùy ý, tập hợp các điểm biểu diễn số phức \(v=z^2-\left(\overline{z}\right)^2\) là đường nào trong mặt phẳng phức ?
Gọi \(z=x+yi\) ta có:
\(v=z^2-\left(\overline{z}\right)^2=\left(x+yi\right)^2-\left(x-yi\right)^2\)
\(=4xyi\)
Phần thực của v luôn bằng 0 nên v nằm trên trục tung.
Kí hiệu \(z_1,z_2,z_3,z_4\) là bốn nghiệm phức của phương trình \(z^4+7z^2+12=0\)
Tính tổng \(T=z^4_1+z^4_2+z^4_3+z^4_4\) ?
Có \(z^4+7z^2+12=0\Leftrightarrow\left(z^2+3\right)\left(z^2+4\right)=0\Leftrightarrow z^2=-3;z^2=-4\Leftrightarrow z_{1,2}=\pm i\sqrt{3};z_{3,4}=\pm2i.\)
Do đó \(z_{1,2}^2=-3,z_{3,4}=-4\Rightarrow z_{1,2}^4=9;z_{3,4}=16.\) Vì vậy \(T=2\left(9+16\right)=50.\)
Kí hiệu i là đơn vị ảo. Trong các khẳng định sau, khẳng định nào đúng ?
Ta có:
\(\left(1+i\right)^2=1+2i+i^2=1+2i-1=2i\)
Vậy: \(\left(1+i\right)^{10}=\left[\left(1+i\right)^2\right]^5=\left(2i\right)^5=32.\left(i^2\right)^2.i=32.\left(-1\right)^2i=32i\)
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức \(z\) thỏa mãn điều kiện \(2\left|z-1-2i\right|=\left|3i+1-2\overline{z}\right|\) ?
Điểm \(M\left(x;y\right)\) biểu diễn số phức \(z=x+yi.\) Điều kiện trong đề bài trở thành
\(2\left|x+yi-1-2i\right|=\left|3i+1-2\left(x-yi\right)\right|\Leftrightarrow2\left|\left(x-1\right)+\left(y-2\right)i\right|=\left|\left(1-2x\right)+\left(3+2y\right)i\right|\)
\(\Leftrightarrow4\left|\left(x-1\right)+\left(y-2\right)i\right|^2=\left|\left(1-2x\right)+\left(3+2y\right)i\right|^2\Leftrightarrow4\left(\left(x-1\right)^2+\left(y-2\right)^2\right)=\left(1-2x\right)^2+\left(3+2y\right)^2\)
\(\Leftrightarrow2x+14y-5=0.\)
Vậy tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức \(z\) thỏa mãn điều kiện \(2\left|z-1-2i\right|=\left|3i+1-2\overline{z}\right|\) là đường thẳng \(2x+14y-5=0\).
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại C. Gọi G là trọng tâm của tam giác ABC. Tính độ dài cạnh AB biết hình lăng trụ đã cho có chiều cao gấp đôi cạnh đáy AC và khối tứ diện GA'B'C' có thể tích bằng \(9cm^3\) ?

Cho khối hộp ABCD.A'B'C'D' có đáy là hình thoi với góc nhọn \(60^o\), chiều cao khối hộp bằng cạnh đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, B'C', C'D'. Tính thể tích V của khối hộp đã cho biết rằng khối tứ diện C'MNP có thể tích \(5cm^3\) ?

Tính cạnh của hình lập phương ABCD.A'B'C'D' biết rằng khối chóp D.ABC'D' có thể tích bằng \(9cm^3\) ?

Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông với độ dài ba cạnh là 3cm, 4cm, 5cm. Gọi \(A_0,B_0,C_0\) lần lượt là trung điểm 3 cạnh bên AA', BB', CC' và \(V_a,V_b,V_c\) theo thứ tự là thể tích các khối chóp \(A_0.BB'CC';B_0.CC'AA';C_0.AA'BB'\). Trong các khẳng định sau, khẳng định nào đúng ?

Tính diện tích toàn phần một khối trục có diện tích xung quanh bằng \(4\pi cm^2\) và thiết diện qua trục là một hình vuông
Gọi 2a(cm) là độ dài cạnh hình vuông thiết diện qua trục thì a là bán kính đáy và diện tích xung quanh khối trụ là:
\(S_{xq}=2a.2\pi a=4\pi a^2\). Theo giả thiết, \(S_{xq}=4\pi\)cm2, suy ra a = 1cm.
Diện tích đáy của khối trụ là \(\pi.1^2=\pi\), diện tích toàn phần là:
\(S_{tp}=S_{xq}+2.S_đ=4\pi+2\pi=6\pi\) m2
Một khối gỗ hình trụ có chiều cao bằng đường kính đáy và có thể tích \(1cm^3\). Người ta khoét khối gỗ bởi hai nửa hình cầu mà đường tròn dáy của khối gỗ là đường tròn lớn của mỗi nửa hình cầu thì phần còn lại có thể tích bao nhiêu ?

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(\sqrt{6}cm\) và SAC là tam giác đều. Tính thể tích khối nón đỉnh S và đáy là đường tròn nội tiếp ABCD ?

Cho hình chóp tứ giác đều S.ABCD có các mặt bên nghiêng với đáy một góc \(60^0\). Tính cạnh đáy của hình chóp biết rằng mặt nón đỉnh S và đáy là đường tròn nội tiếp ABCD có diện tích xung quanh bằng \(50\pi cm^2\) ?

Tính thể tích khối hộp ABCD.A'B'C'D' nếu biết \(A\left(1;1;0\right);A'\left(1;1;3\right);B'\left(2;1;3\right);C\left(2;2;0\right)\) ?

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\left(d\right):\left\{\begin{matrix}x=3\\y=6\\z=4+t\end{matrix}\right.\). Trong các vectơ sau, vectơ nào song song với đường thẳng này ?
(d) có vectơ chỉ phương \(\overrightarrow{v}\left(0;0;1\right)\)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left(P\right):3x-4z-1=0\). Mặt cầu nào trong các mặt cầu dưới đây cắt (P) ?

Viết phương trình của đường thẳng (d) qua điểm A(1;2;3) và vuông góc với mặt phẳng \(\left(P\right):4x+3y-7z+1=0\)

Tìm một vectơ chỉ phương của giao tuyến hai mặt phẳng \(\left(P\right):3x+2y-z-1=0\) và \(\left(Q\right):x+4y-3z+2=0\) ?

Viết phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng
\(\left(P\right):2x+y-z-3=0\)
\(\left(P'\right):x+y+z-1=0\)

Tính khoảng cách giữa hai đường thẳng
\(d:\left\{\begin{matrix}x=-1\\y=-1\\z=t\end{matrix}\right.\) và \(d':\left\{\begin{matrix}x=1\\y=1\\z=t'\end{matrix}\right.\)

Cho mặt phẳng \(\left(P\right):x-y-z-1=0\) và đường thẳng \(d:\frac{x+1}{2}=\frac{y-1}{1}=\frac{z-2}{3}\)
Viết phương trình đường thẳng \(\Delta\) qua A(1;1;-2) vuông góc với d và song song với (P) ?
