Cảnh báo
Bạn cần đăng nhập mới làm được đề thi này
Cho hàm số \(y=f\left(x\right)\) với tập xác định \(D=\left[a;c\right]\) có đồ thị như hình dưới đây :
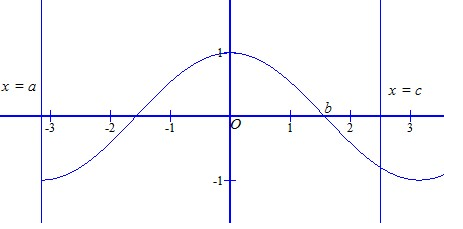
Trong các khẳng định sau, khẳng định nào đúng ?
Cho hàm số \(y=f\left(x\right)\) xác định liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau :
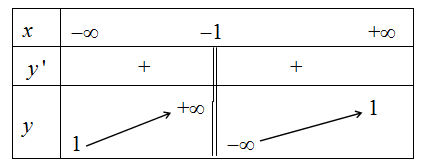
Đường nào trong các đường sau đây có thể là đồ thị của hàm số đã cho ?
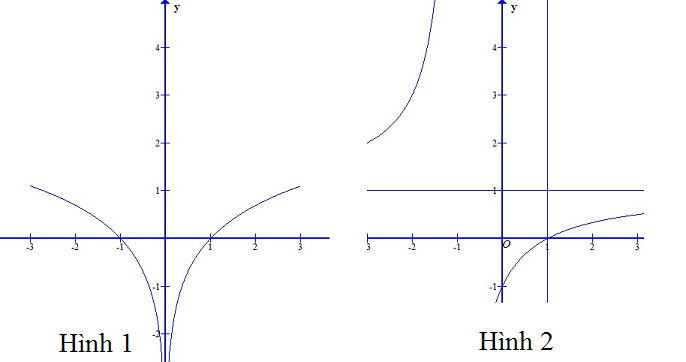
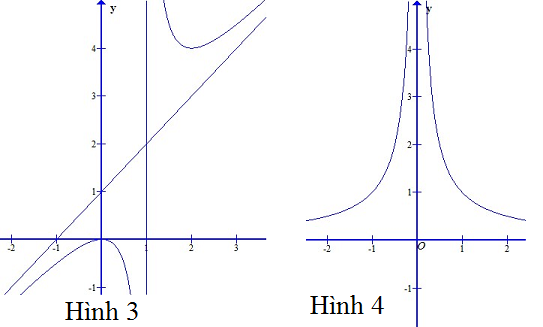
Từ bảng biến thiên ta thấy đồ thị có tiệm cận đứng và tiệm cận ngang nên Hình 1, Hình 3, Hình 4 không phù hợp
Trong các khoảng sau, hàm số \(y=\ln\left|2x-1\right|\) đồng biến trên khoảng nào ?
Hàm số \(y=\ln\left|2x-1\right|\) có \(y'=\dfrac{2}{2x-1}\)
Hàm số đồng biến khi \(y'>0\Leftrightarrow x\in\left(\dfrac{1}{2};+\infty\right)\)
Trong các đường cong cho sau đây, đường nào là đồ thị của hàm số : \(y=\frac{x-2}{2x+1}\) ?


\(\lim\limits_{x\rightarrow-\frac{1}{2}}y=\infty;\lim\limits_{x\rightarrow\infty}y=\frac{1}{2}\)
Hàm số có tiệm cận đứng \(x=-\frac{1}{2}\); tiệm cận ngang \(y=\frac{1}{2}\)
Tìm giá trị cực tiểu của hàm số \(y=\sin2x\)
Ta có \(y=\sin2x;y'=2\cos2x;y"=-4\sin2x\)
\(y'=0\Leftrightarrow\cos2x=0\) \(\Leftrightarrow2x=\pm\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{4}+k\pi,\left(k\in \mathbb{Z}\right)\)
Mà \(y"\left(\pm\dfrac{\pi}{4}+k\pi\right)=-4\sin\left(\pm\dfrac{\pi}{4}+k\pi\right)=\mp4\)
Các điểm cực tiểu của hàm số là : \(x=-\dfrac{\pi}{4}+k\pi\)
Các giá trị cực tiểu là \(y\left(-\dfrac{\pi}{4}+k\pi\right)=\sin\left(-\dfrac{\pi}{4}+k\pi\right)=-1\)
Cách khác: Hàm số \(y=\sin2x\) liên tục trên toàn trục số, có GTLN \(=1\), GTNN \(=-1\)cũng đồng thời là giá trị cực đại và giá trị cực tiểu. Vì vậy đáp số đúng là \(y=-1.\)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(y=x+\cos x\) trên đoạn \(\left[\dfrac{\pi}{6};\dfrac{5\pi}{3}\right].\)
\(y'=0\Leftrightarrow1-\sin x=0\)
Trong khoảng \(\left(\dfrac{\pi}{6};\dfrac{5\pi}{3}\right)\) phương trình \(y'=0\) chỉ có nghiệm là \(x=\dfrac{\pi}{2}\)
Giá trị của \(y=x+\cos x\) tại \(\dfrac{\pi}{6};\dfrac{\pi}{2};\dfrac{5\pi}{3}\) lần lượt là \(\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2};\dfrac{\pi}{2};\dfrac{5\pi}{3}+\dfrac{1}{2}\)
Do đó : \(\max_Dy=\dfrac{5\pi}{3}+\dfrac{1}{2};\min_Dy=\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}\)
Tìm hoành độ các giao điểm của đường thẳng \(y=2x-\frac{13}{4}\) với đồ thị hàm số \(y=\frac{x^2-1}{x+2}\) ?
Phương trình \(y=2x-\frac{13}{4}=\frac{x^2-1}{x+2}\) có 2 nghiệm \(x=2;x=-\frac{11}{4}\)
Tìm các giá trị của tham số m để đồ thị hàm số \(y=\frac{x^2+\left(m+2\right)x+m^2+2}{x+m}\) có hai điểm cực trị cách đều trục tung.
Cần tìm m để \(y'=\dfrac{x^2+2mx+2m-2}{\left(x+m\right)^2}\) có 2 nghiệm phân biệt với tổng bằng 0.
Điều kiện \(x_1+x_2=0\Leftrightarrow-2m=0\Leftrightarrow m=0\). Thử lại: khi \(m=0\) thì \(y'=\dfrac{x^2-2}{x^2}\) có 2 nghiệm phân biệt \(x=\pm\sqrt{2}\), đồ thị hàm số có 2 điểm cực trị cùng cách trục tung một khoảng bằng \(\sqrt{2}.\)
Đồ thị hàm số \(y=\dfrac{\sqrt{x^2-4}+1}{x^2+1}\) có bao nhiêu đường tiệm cận (đứng, ngang) ?
Vì \(y=\dfrac{\sqrt{x^2-4}+1}{x^2+1}=\dfrac{\left|x\right|\sqrt{1-\dfrac{4}{x^2}}+1}{\left|x\right|^2+1}=\dfrac{\dfrac{1}{\left|x\right|}\sqrt{1-\dfrac{4}{x^2}}+\dfrac{1}{\left|x\right|^2}}{1+\dfrac{1}{\left|x\right|^2}}\) nên \(\lim\limits_{x\rightarrow\infty}y=0\) do đó đồ thị có 1 tiệm cận ngang là \(y=0.\)
Vì hàm số xác định với \(x\le-4\) hoặc \(x\ge4\) và \(y\left(\pm4\right)=\dfrac{1}{17}\) nên hàm số không có tiệm cận đứng.
Kí hiệu M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=2\sin x+\sin2x\) trên đoạn \(\left[0;\dfrac{3\pi}{2}\right]\). Tính \(M^m\)
\(y'=2\cos x+2\cos2x=4\cos\dfrac{x}{2}\cos\dfrac{3x}{2}\). Trong khoảng \(\left(0;\dfrac{3\pi}{2}\right)\) phương trình \(y'=0\) có đúng hai nghiệm \(x=\dfrac{\pi}{3}\) và \(x=\pi\).
Giá trị hàm số tại \(x=0;x=\dfrac{\pi}{3};x=\pi;x=\dfrac{3\pi}{2}\) lần lượt là \(0;\dfrac{3\sqrt{3}}{2};0;-2\)
Do đó \(M=\dfrac{3\sqrt{3}}{2};m=-2\) nên \(M^m=\dfrac{4}{27}\)
Tìm các giá trị thực của tham số \(m\) sao cho hàm số \(y=mx^4+\left(m^2-9\right)x^2+10\) có ba điểm cực trị.
Có \(y'=4mx^3+2\left(m^2-9\right)x=2x\left[2mx^2+m^2-9\right]\)
Cần tìm \(m\) để \(y'\) có ba nghiệm phân biệt, tức là tam thức bậc hai \(2mx^2+m^2-9\) phải có hai nghiệm phân biệt khác \(0\).
Vậy phải có \(\dfrac{-m^2+9}{2m}>0\).Tức là \(m< -3;0< m< 3\).
Tính tổng các nghiệm của phương trình \(2^{x^2-3}.5^{x^2-3}=0,01\left(10^{x-1}\right)^3\)
Viết lại phương trình thành \(10^{x^2-3}=10^{3x-5}\) hay \(x^2-3=3x-5\). Phương trình có 2 nghiệm \(x=1;x=2\). Tổng các nghiệm là 3
Tính đạo hàm của hàm số \(y=\left(-x+1\right)^{-\frac{1}{3}}\)
Sử dụng công thức \(\left(u^{\alpha}\right)'=\alpha u^{\alpha-1}u'\)
Tìm tập xác định \(D\) của hàm số \(y=\left(x^2+x-2\right)^{-2}\) .
\(y=\left(x^2+x-2\right)^{-2}=\dfrac{1}{\left(x^2+x-2\right)^2}\)
Hàm số xác định khi và chỉ khi
\(x^2+x-2\ne0\Leftrightarrow x\ne1;x\ne-2\)
Giải bất phương trình \(4^x-2.5^{2x}< 10^x\)
\(4^x-2.5^{2x}< 10^x\)
\(\Leftrightarrow2^{2x}-2.5^{2x}< 2^x.5^x\)
\(\Leftrightarrow\frac{2^{2x}}{5^{2x}}-2< \frac{2^x}{5^x}\)
Đặt \(t=\left(\frac{2}{5}\right)^x;t>0\)
\(t^2-t-2< 0\)
\(\Leftrightarrow-1< t< 2\)
Đối chiếu với điều kiện của t ta có:
\(\left(\frac{2}{5}\right)^x< 2\)
\(\Leftrightarrow x>\log_{\frac{2}{5}}2\) (vì cơ số \(\frac{2}{5}< 1\))
Cho hàm số \(f\left(x\right)=\ln\left(4x-x^2\right)\). Khẳng định nào trong các khăng định sau đây đúng ?
\(f'\left(x\right)=\frac{4-2x}{4x-x^2}\Rightarrow f'\left(2\right)=0\)
Cho \(\log_{a^2+2}27=b^2+1\). Hãy tính \(\log_{\sqrt{3}}\sqrt[6]{a^2+2}\) ?
Sử dung công thức đổi cơ số ta có :
\(\log_{\sqrt{3}}\sqrt[6]{a^2+1}=\frac{\log_{a^2+1}\sqrt[6]{a^2+1}}{\log_{a^2+1}\sqrt{3}}=\frac{\frac{1}{6}}{\frac{1}{2}\log_{a^2+1}3}=\frac{1}{3\log_{a^2+1}3}=\frac{1}{\log_{a^2+1}27}=\frac{1}{b^2+1}\)
Tính đạo hàm của hàm số \(y=5x^2-2^x\cos x\) ?
Cho a, b, c là ba số dương thỏa mãn điều kiện \(a,b,ab\ne1\). Trong các khẳng định sau, khẳng định nào đúng ?
Ta có \(\frac{\log_ac+\log_bc}{\log_ac.\log_bc}=\frac{1}{\log_bc}+\frac{1}{\log_ac}=\log_cb+\log_ca=\log_c\left(ab\right)=\frac{1}{\log_{ab}c}\)
Suy ra \(\log_{ab}c=\frac{\log_ac.\log_bc}{\log_ac+\log_bc}\)
Xét phương trình \(5^x.2^{\frac{2+x}{x}}=40\) (*). Trong các khẳng định,khẳng định nào sai ?
\(5^x.2^{\frac{2+x}{x}}=40\)
\(\Leftrightarrow5^x.2^{\frac{2+x}{x}}=5.2^3\)
\(\Leftrightarrow\frac{5^x}{5}=\frac{2^3}{2^{\frac{2+x}{x}}}\)
\(\Leftrightarrow5^{x-1}=2^{3-\frac{2+x}{x}}\)
\(\Leftrightarrow5^{x-1}=2^{\frac{2x-2}{x}}\)
\(\Leftrightarrow5^{x-1}=2^{\frac{2\left(x-1\right)}{x}}\)
\(\Leftrightarrow5^{x-1}=4^{\frac{x-1}{x}}\)
\(\Leftrightarrow5^{x-1}=\left(4^{\frac{1}{x}}\right)^{x-1}\)
\(\Leftrightarrow\ln5^{x-1}=\ln\left(4^{\frac{1}{x}}\right)^{x-1}\)
\(\Leftrightarrow\left(x-1\right)\ln5=\left(x-1\right).\frac{1}{x}\ln4\)
\(\Leftrightarrow\left(x-1\right)\left[\ln5-\frac{\ln4}{x}\right]=0\)
\(\Leftrightarrow\left[\begin{matrix}x=1\\x=\frac{\ln4}{\ln5}\end{matrix}\right.\)
Tìm tất cả các giá trị của tham số m để bất phương trình sau được nghiệm đúng với mọi x:
\(9^x-m.3^x-m+3>0\)
Đặt \(t=3^x\left(t>0\right)\) thì bất phương trình trở thành \(t^2+3>m\left(t+1\right)\Leftrightarrow m< \frac{t^2+3}{t+1}\)
Cần tìm m nhỏ hơn mọi giá trị của hàm \(f\left(t\right)=\frac{t^2+3}{t+1}\left(t>0\right)\)
Ta có \(f'\left(t\right)=\frac{t^2+2t-3}{\left(t+1\right)^2}\)
Trong khoảng \(\left(0;+\infty\right)\) đạo hàm chỉ triệt tiêu tại t = 1.
Chú ý rằng \(f\left(0\right)=3;f\left(1\right)=2;\lim\limits_{t\rightarrow+\infty}f\left(t\right)=+\infty\) nên \(min_{t\in\left(0;+\infty\right)}f\left(t\right)=2\)
Với e là cơ số của logarit tự nhiên, trong các khẳng định sau, khẳng định nào sai ?
Tìm hàm F(x) biết \(F'\left(x\right)=\sin2x\) và \(F\left(\frac{\pi}{2}\right)=1\) ?
\(F\left(x\right)\) là nguyên hàm của \(\sin2x\) nên \(F\left(x\right)=-\frac{1}{2}\cos2x+C\), \(F\left(\frac{\pi}{2}\right)=C+\frac{1}{2}\). Do đó điều kiện \(F\left(\frac{\pi}{2}\right)=1\Leftrightarrow C=\frac{1}{2}\) nên \(F\left(x\right)=-\frac{1}{2}\cos2x+\frac{1}{2}\)
Hai viên đạn cùng rời khỏi nòng súng tại thời điểm t = 0 với những vận tốc khác nhau :
- Viên đạn thứ nhất có vận tốc \(u\left(t\right)=3t^2\) (m/s)
- Viên đạn thứ hai có vận tốc \(v\left(t\right)=2t+5\) (m/s)
Hỏi từ giây thứ mấy thì viên đạn thứ nhất xa điểm xuất phát hơn viên đạn thứ hai ?
Từ ý nghĩa cơ học của đạo hàm suy ra tại thời điểm \(t=t_o\) hai viên đạn cách nòng súng lần lượt là :
\(s_1=\int\limits^{t_0}_03t^2\text{dt}=t_0^3\)
\(S_2=\int\limits^{t_0}_0\left(2t+5\right)dt=t_0^2+5t_0\)
Tìm ra nghiệm dương của bất phương trình
\(s_1>s_2\Leftrightarrow t^3_0>t^2_0+5t_0\Leftrightarrow t^2_0-t_0-5>0\)
Ta được \(t_0>\frac{1+\sqrt{21}}{3}\approx2,79\)
Do đó từ giây thứ 3 viên đạn thứ nhất xa điểm xuất phát hơn viên đạn thứ hai
Đặt \(I=\int\limits^3_1\frac{dx}{e^x-1}\) và \(t=e^x-1\)
Khẳng định nào trong các khẳng định sau là sai ?
Tính \(I=\int\limits^{\left(\frac{\pi}{2}\right)^2}_0\cos\sqrt{x}dx\) ?
Đổi biến \(t=\sqrt{x}\) rồi tích phân từng phần ta có :
\(\int\limits^{\left(\frac{\pi}{2}\right)^2}_0\cos\sqrt{x}dx=\int\limits^{\frac{\pi}{2}}_0\cos t.2tdt=\int\limits_0^{\frac{\pi}{2}}2td\sin t=2t\sin t|^{\frac{\pi}{2}}_0-\int\limits^{\frac{\pi}{2}}_0\sin td2t=\pi-2\)
Tính diện tích hình phẳng giới hạn bởi các đường \(y=2\sin x;y=1+\cos^2x;x=0;x=\pi\) ?
\(S=\int\limits^{\pi}_0\left|1+\sin x-\cos^2x\right|dx\)
\(=\int\limits^{\pi}_0\left|\sin x+\sin^2x\right|\text{d}x\)
\(=\int\limits^{\pi}_0\left(\sin x+\sin^2x\right)\text{d}x\)
\(=\int\limits^{\pi}_0\sin x\text{d}x+\int\limits^{\pi}_0\frac{1}{2}\left(1-\cos2x\right)\text{d}x\)
\(=-\cos x|^{\pi}_0+\frac{1}{2}x|^{\pi}_0-\frac{1}{4}\sin2x|^{\pi}_0\)
\(=2+\frac{\pi}{2}\)
Tính thể tích khối tròn xoay sinh ra khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi hai đồ thị \(y=x^2-4x+6\) và \(y=-x^2-2x+6\) .
\(V=\left|\pi\int\limits^1_0\left[\left(x^2-4x+6\right)^2-\left(-x^2-2x+6\right)^2\right]dx\right|\)
\(=\left|\pi\int\limits^1_0\left(-12x^3+36x^2-24x\right)dx\right|\)
\(=\pi\left|\left(-3x^4+12x^3-12x^2\right)|^1_0\right|=\pi\left|-3\right|=3\pi\)
\(V=3\pi\)
Cho hai số phức \(z_1=3-4i;z_2=4+3i\). Tính \(\left|\frac{2z_1}{3z_2}\right|\) ?
Sử dụng định nghĩa phép chia 2 số phức và định nghĩa mô đun của một số phức.
Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện \(z^2\) có điểm biểu diễn nằm trên trục hoành ?
Nếu \(z=z+yi\) thì \(z^2=x^2-y^2+2xyi\)
Nếu \(z^2\) có điểm biểu diễn thuộc trục hoành thì
\(2xy=0\Leftrightarrow\left[\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Đây là phương trình 2 trục tọa độ
Có bao nhiêu cặp số thực (x, y) thỏa mãn điều kiện :
\(\left(x^2-3x\right)+\left(5y^2+y+1\right)i=\left(y+1\right)+\left(y^2+2y+6\right)i\)
Giải hệ phương trình \(\left\{\begin{matrix}x^2-3x=y+1\\5y^2+y+1=y^2+2y+6\end{matrix}\right.\)
hay \(\left\{\begin{matrix}4y^2-y-5=0\\y=x^2-3x-1\end{matrix}\right.\)
Hệ có 4 nghiệm
Kí hiệu i là đơn vị ảo. Trong các khẳng định sau, khẳng định nào sai ?
\(i^2=-1;i^3=-i;i^4=1;i^5=i\)
Do đó mọi \(k\in Z\); \(i^{4k}=1;i^{4k+1}=i;i^{4k+2}=-1;i^{4k+3}=-i\)
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức \(z\) thỏa mãn điều kiện \(\left|z\left(i+1\right)-1-i\right|=\sqrt{2}\)
Nếu \(z=x+yi\) thì \(z\left(i+1\right)-1-i=\left(x-1-y\right)+\left(x-1+y\right)i\)
Do đó điều kiện cho trong đề bài trở thành \(\left(x-1-y\right)^2+\left(x-1+y\right)^2=2\) hay \(\left(x-1\right)^2+y^2=1\)
Cho hình lập phương ABCD.A'B'C'D'. Đường chéo A'C của hình lập phương cắt mặt phẳng (AB'D') tại điểm E. Tính thể tích hình lập phương biết rằng đoạn A'E có độ dài \(\sqrt{3}\) cm ?

Cho hình thoi với góc nhọn bằng \(45^o\). Một khối lăng trụ có thể tích \(1000cm^3\), đáy là hình thoi đã cho, cạnh bên gấp đôi cạnh đáy và tạo với mặt phẳng một góc \(45^o\). Tính cạnh bên khối lăng trụ ?

Cho khối lăng trụ tam giác đều ABC.A'B'C' có thể tích bằng 27 \(cm^3\). Đường thẳng đi qua trọng tâm của tam giác ABC song song với BC cắt AB, AC lần lượt tại D, E. Tính thể tích khối tứ diện AA'DE ?

Cho hình chóp S.ABCD có đáy là hình chữ nhật với hai kích thước \(AB=a;AD=2a\), cạnh bên SA vuông góc với đáy. Mặt phẳng (SBC) phải tạo với đáy một góc bao nhiêu độ để khối chóp đã cho có thể tích \(\frac{2a^3}{3}\) ?
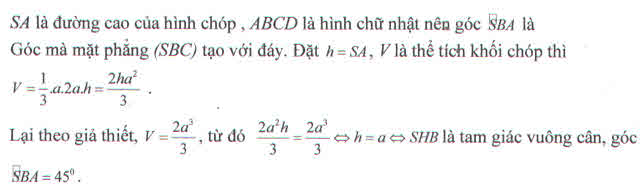
Cho khối lăng trụ tam giác đều ABC.A'B'C' có thể tích \(3\sqrt{3}cm^3\) và có chiều cao gấp đôi cạnh đáy. Xét khối trụ với hai đường tròn đáy là hai đường tròn nội tiếp hai tam giác ABC; A'B'C'. Tính thể tích hình trụ nằm trong khối lăng trụ đã cho ?

Để đổ 1 cây cột cầu hình trụ đường kính 1m và cao 5m cần bao nhiêu khối bê tông ? (cho biết \(\pi=3,14\))
\(V=h\pi R^2\) với \(h=5m;R=\frac{1}{2}m\)
Từ đó \(V=\frac{5\pi}{4}\approx3,925m^3\)
Tính thể tích khối nón ngoại tiếp khối chóp tứ giác đều S.ABCD có cạnh đáy bằng \(\sqrt{6}\) cm và SAC là tam giác đều ?

Tính diện tích xung quanh một hình nón có tâm của đáy cách đường sinh một khoảng \(\sqrt{3}cm\) và thiết diện qua trục hình nón là một tam giác đều.

Cho 3 điểm \(A\left(2;1;1\right);B\left(1;-1;0\right);C\left(1;0;2\right)\). Tính độ dài đường chéo hình hộp nhận OA, OB, OC làm 3 cạnh.

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\left(d\right):\frac{x-2}{3}=\frac{y+1}{-2}=\frac{z-1}{1}\)
Vectơ nào trong các vectơ sau đây song song với (d) ?
Vecto chỉ phương của d là (3;-2;1).
Chỉ có vectơ trong \(\overrightarrow{u}\left(6;-4;2\right)\) có các tọa độ tỉ lệ với bộ 3 số (3; -2; 1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left(P\right):3x-4z-1=0\). Mặt cầu nào trong các mặt cầu sau đây tiếp xúc với (P) ?

Viết phương trình mặt phẳng qua điểm \(M\left(0;0;-1\right)\) và song song với hai đường thẳng :
\(d_1:\frac{x}{1}=\frac{y-2}{-2}=\frac{z-3}{3}\)
\(d_2:\left\{\begin{matrix}x=1+3t\\y=2\\z=-1+5t\end{matrix}\right.\)
Tọa độ M không thỏa mãn các phương trình cho trong
\(5x-2y-3z-21=0\)
\(5x-2y-3z+21=0\)
\(10x-4y-6z+21=0\)
Vậy chọn
\(-5x+2y+3z+3=0\)
Tìm tọa độ giao điểm đường thẳng :
\(d:\frac{x+1}{1}=\frac{y}{-1}=\frac{z+2}{3}\) với mặt phẳng \(\left(P\right):x+2y-z-3=0\)
Tham số hoá đường thẳng d:
\(\left\{\begin{matrix}x=-1+t\\y=-t\\z=-2+3t\end{matrix}\right.\)
Thay vào phương trình (P) tìm được t rồi xác định được giao điểm.
Viết phương trình mặt phẳng chứa hai điểm \(A\left(1;0;0\right);B\left(0;-2;3\right)\) và cách điểm \(M\left(1;1;1\right)\) một khoảng bằng \(\frac{2}{\sqrt{3}}\) ?
Tính độ dài đoạn vuông góc chung của hai đường thẳng \(d:\left\{\begin{matrix}x=1\\y=t\\z=2t\end{matrix}\right.\) và đường thẳng d' xác định bởi \(\left\{\begin{matrix}2y-z=0\\x=5\end{matrix}\right.\)
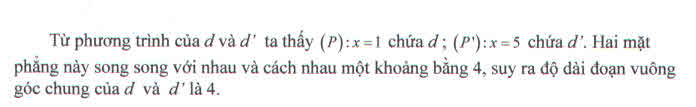
Cho đường thẳng d xác định bởi \(\left\{\begin{matrix}x-y=1\\y+z=0\end{matrix}\right.\) và mặt phẳng \(\left(P\right):x+y+2z-1=0\). Trong các khẳng định sau, khẳng định nào đúng ?

Gọi \(\mathbb{R}\) là tập các số thực, \(\mathbb{C}\) là tập các số phức. Tìm khẳng định sai:
\(z=-11\in\mathbb{R}\subset\mathbb{C}\)