Cung và góc liên kết
Nội dung lý thuyết
Các phiên bản khácCUNG VÀ GÓC LIÊN KẾT
a) Cung đối nhau: α và (-α)
sin(-α) = -sinα tan(-α) = -tanα
cos(-α) = cosα cot(-α) = -cotα
b) Cung bù nhau: α và π – α
sin(π – α) = sinα tan(π – α) = -tanα
cos(π – α) = -cosα cot(π – α) = -cotα
c) Cung hơn nhau π: α và π + α
sin(π + α) = -sinα tan(π + α) = tanα
cos(π + α) = -cosα cot(π + α) = cotα
d) Cung phụ nhau: α và (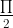 – α)
– α)
sin( – α) = cosα tan(
– α) = cosα
cos( – α) = sinα cot(
– α) = tanα