ta có : góc DBA + góc ABC = 180 độ

           góc ACB + góc ACE = 180 độ 

           mà góc ABC = góc ACB ( ABC cân tại A)

       =) góc ABD = góc ACE

xét tam giác ADB và tam giác AEC có :

           góc ABD = góc ACB

                DB=CE

               AB = AC

        ADB = AEC (c-g-c)

         =) góc BAD = góc  CAE

 Ta có: MD vuông góc với BE
              BE vuông góc với EN
=>MD//EN => góc DMI = góc INE(so le trong)
Xét tam giác MDI và tam giác IEN ta có:
MD=EN(vì tam giác MBD = tam giác CEN)
góc MDI = góc IEN(=90 độ)
góc DMI = góc INE(cmt)
=>tam giác MDI = tam giác IEN(CGV-GN)
=>IM=IN(ctư)
=>đường thẳng BC cắt MN tại trung điểm I của MN

:D

khó thể xem trên mạng

Tam giác ABC cân tại A => AB = AC

=> Góc ABD = góc ACE

Xét tam giác ABD và tam giác ACE

AB = AC ( cmt )

Góc ABD = góc ACE ( cmt )

BD = CE ( gt )

=> Tam giác ABD = tam giác ACE ( c.g.c )

=> Góc BAD = góc CAE ( 2 góc tương ứng )

=> AD = AC ( 2 cạnh tương ứng )

Xét tam giác ADE và tam giác ACE

AD = AC ( cmt )

DE = EC( gt )

AE chung

=> tam giác ADE= tam giác ACE ( c.c.c )

=> góc DAE = góc EAC ( 2 góc tương ứng )

Ta có: góc BAD = góc EAC ( cmt )

Góc DAE = góc EAC ( cmt )

=> góc BAD = góc DAE = góc EAC

a) Ta có: tam giác ABC cân tại A (gt)

=> Góc B = góc C₁, AB = AC (định lí)

Xét tam giác ABD và tam giác ACE có:

AB = AC (chứng minh trên)

BD = CE (gt)

Góc B = góc C₁ (chứng minh trên)

=> Tam giác ABD = tam giác ACE (c.g.c)

=> Góc BAD = góc CAE (2 góc tương ứng)   (đpcm)

b) Ta có: tam giác ABD = tam giác ACE (chứng minh trên)

=> AB = AC (2 cạnh tương ứng)

Xét tam giác ADE và tam giác CEK có:

DE = CE (gt)

Góc AED = góc CEK (2 góc đối đỉnh)

AE = EK (gt)

=> Tam giác ADE = tam giác CKE (c.g.c)

=> AD = CK (2 cạnh tương ứng)

Kẻ đường cao AH 

Ta có: DH < AH

=> AD < AB mà AB = AC (chứng minh trên)

=> AC > AD   (đpcm)

c) Ta có: AD < AC

Mà AD = CK (2 cạnh tương ứng)

=> CK < AC

Xét tam giác ACK có AC > CK

=> Góc CAK < góc K (định lí)

Lại có: góc BAD = góc CAE (chứng minh trên)

=> Góc BAD < góc K

Mà góc K = DAE (vì tam giác ADE = tam giác KCE)

=> Góc BAD < góc DAE

hay góc BAD = góc CAE < góc DAE   (đpcm)

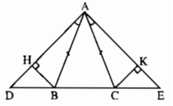
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)

Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)

∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)

Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE

+) Xét ΔABD và ΔACE có:

∠DAB = ∠EAC ( giả thiết)

AB = AC (vì tam giác ABC cân tại A)

∠ABD = ∠ACE ( chứng minh trên )

⇒ ΔABD = ΔACE (g.c.g)

⇒ BD = CE ( hai cạnh tương ứng)..

a) Do ΔABC cân tại A

=> AB = AC; góc ABC=góc ACB

Lại có: góc ABC+ góc ABD = 180^o (kề bù)

góc ACB + góc ACE = 180^o (kề bù)

=> góc ABD = góc ACE

Xét ΔADB và ΔAEC có:

góc BAD = góc CAE (gt)

AB = AC (cmt)

góc ABD = góc ACE (cmt)

=> ΔADB = ΔAEC (g.c.g)

=> BD = CE (2 cạnh tg ứng) đpcm

b) Vì ΔADB = ΔAEC (câu a)

=> góc ADB = góc AEC (2 góc t/ư)

hay góc HDB = góc KEC

Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:

BD = CE (câu a)

góc HDB = góc KEC(cmt)

=> ΔBHD = ΔCKE (ch - gn)

=> BH = CK (2 cạnh tg ứng) (đpcm)

đây e ơi https://olm.vn/hoi-dap/question/541217.html

Em tham khảo tại link dưới đây nhé.

Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

nếu cậu biết câu c mách tớ

nhanh lên tớ cần gấp trong hôm nay

NHANH LÊN NHÉ!!!

a/ Xét 2 tam giác MDC và MAB có MA=MD (gt), MB=MC (gt), góc DMC=góc AMB (đối đỉnh)

=> tam giác MDC = tam giác MAB

=> Góc CBA=góc BCD (Góc tương ứng)

Xét \(\Delta ABC\)có \(\widehat{CBA}+\widehat{ACB}=90^0\)(Tính chất Tam giác vuông)

=> \(\widehat{BCD}+\widehat{ACB}=90^0=\widehat{ACD}\) => \(CD\perp AC\)

b/ Xét 2 tam giác vuông CHE và CHA có: CH (chung); HE=HA (gt); Tam giác vuông tại H

=> \(\Delta CHE=\Delta CHA\)=> CA=CE (2 cạnh tương ứng) => \(\Delta CAE\)cân tại C