Tìm x,y thuộc Z sao cho
a)xy=x+y
b)xy=x-y
c)x(y+2)+y=1
d)/x/+/y/=2
1. Tìm x;y sao cho : xy+1 = x + y
2.Tìm x;y thuộc Z sao cho : x + y = xy
1) = xy +1 -x -y =0
y(x-1) -(x-1) = (x-1)(y-1)=0
x =1
y=1
các bn giỏi toán thân mến,các bn hỏi toán đã biến chúng ta thành osin ,làm k công,chúng ta cứ cày đầu giải còn năn nỉ công nhận,
tui nghĩ chất sám có giá trị cao nhât nên chỉ giải cho các bn giỏi hieu ,còn lại k cần năn nỉ loại ngu công nhận vi chúng chẳng hieu j,
học toán mà k chịu suy nghĩ thi còn lâu moi giỏi
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Tìm x,y thuộc Z sao cho \(x^2+xy+y^2=x+y\)
\(x^2+xy+y^2=x+y\)
\(\Leftrightarrow2x^2+2xy+2y^2-2x-2y=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)=2\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2=2\)
Tới đây do \(2=1^2+1^2+0^2\) , đồng thời để ý rằng vai trò \(x,y\) như nhau nên ta sẽ có 2TH
TH1: \(x+y=0\) và \(\left(x-1\right)^2+\left(y-1\right)^2=1^2+1^2\) (1)
khi đó \(y=-x\) nên \(x-1\ne y-1\). Do đó từ (1), giả sử \(x\ge y\) suy ra \(\left\{{}\begin{matrix}x-1=1\\y-1=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\), vô lí. Làm tương tự với \(y\ge x\)
TH2: \(x+y\ne0\). Khi đó \(x+y=\pm1\).
TH2.1: \(x+y=1\). Khi đó từ (1), suy ra 1 trong 2 số \(x-1,y-1\) phải bằng 0. Do vai trò x, y như nhau nên giả sử \(x-1=0\)\(\Leftrightarrow x=1\), khi đó \(y=0\), thỏa mãn. Ta tìm được nghiệm \(\left(x;y\right)=\left(1;0\right)\). Tương tự, tìm được nghiệm \(\left(x;y\right)=\left(0;1\right)\)
TH2.2: \(x+y=-1\). Giả sử \(x-1=0\) \(\Leftrightarrow x=1\), khi đó \(y=-2\), loại.
Như vậy, pt đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(0;1\right);\left(1;0\right)\right\}\)
Cách thứ 2 nhé:
\(x^2+xy+y^2=x+y\)
\(\Leftrightarrow x^2+\left(y-1\right)x+y^2-y=0\)
\(\Delta=\left(y-1\right)^2-4\left(y^2-y\right)\) \(=\left(y-1\right)^2-4y\left(y-1\right)\) \(=\left(y-1\right)\left[\left(y-1\right)-4y\right]\) \(=\left(y-1\right)\left(-1-3y\right)\).
Để pt đã cho có nghiệm thì \(\Delta=-\left(y-1\right)\left(3y+1\right)\ge0\) \(\Leftrightarrow\left(y-1\right)\left(3y+1\right)\le0\) \(\Leftrightarrow-\dfrac{1}{3}\le y\le1\). Do \(y\inℤ\) nên \(y\in\left\{0;1\right\}\). Nếu \(y=0\) thì thay vào pt đầu, dễ dàng suy ra \(x=1\). Còn nếu \(y=1\) thì cũng dễ dàng suy ra \(x=0\).
Vậy ohương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(0;1\right);\left(1;0\right)\right\}\)
Giúp mình vs
Tìm x,y thuộc Z
a)49-y^2=6(x-2021)^2
b)x^2 + xy + y^2=2x+y
c)x^2 + xy + y^2=x+y
d)x^2 + 3xy + 3y^2 =3y
e)x^2 - 2xy - 5y^2=y+1
Bài b:
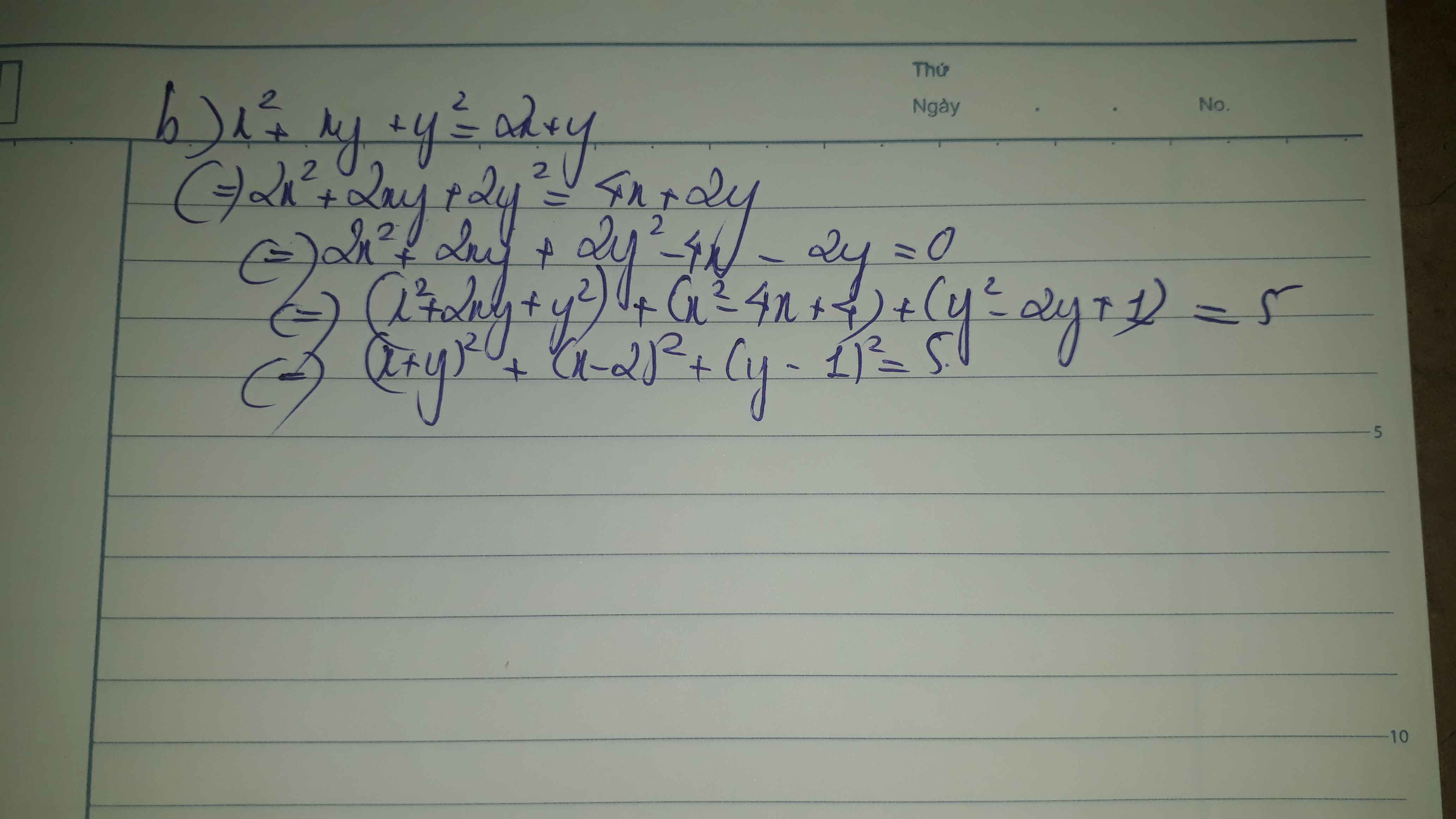
Đến đoạn này bạn xét như bài a nhé.
Bài c cũng tương tự câu b, bạn nhân 2 vào cả 2 vế, chuyển vế đổi dấu và ghép vế trái lại thành tổng các bình phương, vế phải là một số tự nhiên. Đến đoạn này cũng xét như bài a.
Còn bài d và bài e thì mình chưa biết làm thế nào, nhưng mình nghĩ vế trái sẽ là bình phương của tổng hoặc hiệu của x và y, vế phải là bình phương của tổng hoặc hiệu của y và một số nào đó. Tuy nhiên chắc là sẽ phải nhân thêm một số nào đó bởi vì nếu không nhân khi làm sẽ ra phân số, không xét được.