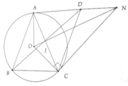
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt AD tại N. Chứng minh rằng :
a) AD là tiếp tuyến của đường tròn
b) Ba đường thẳng AC, BD,ON đồng quy
Cho tam giác ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh:
a, Đường thẳng AD là tiếp tuyến của (O)
b, Ba đường thẳng AC, BD và ON đồng quy
a, Tam giác ABC cân tại A nội tiếp (O)
=> OA ⊥ BC
=> OA ⊥ AD (vì AD//BC)
=> AD là tiếp tuyến của (O)
b, Chứng minh được ON là tia phân giác của A O D ^ mà ∆OAC cân tại O nên ON cũng là đường trung tuyến => ON cắt AC tại trung điểm I của AC => ON,AC,BD cùng đi qua trung điểm I của AC
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt AD tại N. Chứng minh rằng :
a) AD là tiếp tuyến của đường tròn
b) Ba đường thẳng AC, BD,ON đồng quy
a ) OA \(\perp\)BC
BC // AD
=> OA \(\perp\)AD => AD là tiếp tuyến tại A của đường tròn
b) ON cắt AC tại trung điểm của AC ( ON \(\perp\)AC sử dụng đường kính và dây đường tròn )
Lại có : ABCD là hình bình hành
=> BD cắt AC tại trung điểm của AC
=> Ba đường thẳng AC, BD,ON đồng quy
Chỉ là cách làm thôi bạn tự bổ sung nhé !
a ) OA \perp⊥BC
BC // AD
=> OA \perp⊥AD => AD là tiếp tuyến tại A của đường tròn
b) ON cắt AC tại trung điểm của AC ( ON \perp⊥AC sử dụng đường kính và dây đường tròn )
Lại có : ABCD là hình bình hành
=> BD cắt AC tại trung điểm của AC
=> Ba đường thẳng AC, BD,ON đồng quy
Chỉ là cách làm thôi bạn tự bổ sung nhé !
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Vẽ hình bình hành ABCD. Tiếp tuyến tại C cắt đường thẳng AD tại M. CM rằng:
a) AD là tiếp tuyến của đường tròn tâm (O).
b) Ba đường thẳng AC, BD, OM đồng quy
cho tam giác ABC cân tại A nội tiếp đường tròn (O) .Vẽ hình bình hành ABCD tiếp tuyến tại C cắt đường thẳng AD tại M Cmr:
a) AD là tiếp tuyến của (O)
b) Ba đường thẳng AC, BD, OM đồng quy
a) Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Vì O là tâm (ABC) \(\Rightarrow OB=OC\Rightarrow OA\) là trung trực BC
\(\Rightarrow OA\bot BC\) mà \(BC\parallel AD\Rightarrow AD\bot OA\) \(\Rightarrow AD\) là tiếp tuyến
b) MO cắt AC tại E.
Vì MC,MA là tiếp tuyến \(\Rightarrow\Delta MAC\) cân tại M và MO là phân giác \(\angle AMC\)
\(\Rightarrow E\) là trung điểm AC
Vì ABCD là hình bình hành có E là trung điểm AC \(\Rightarrow B,E,D\) thẳng hàng
\(\Rightarrow AC,BD,OM\) đồng quy tại E
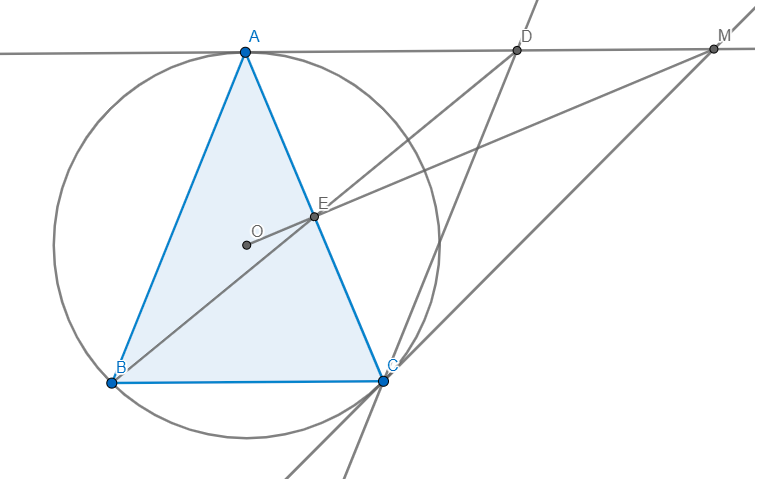
Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $(O)$. Các tiếp tuyến của đường tròn vẽ từ $A$ và $C$ cắt nhau tại $M$. Trên tia $AM$ lấy điểm $D$ sao cho $AD = BC$. Chứng minh rằng:
a) Tứ giác $ABCD$ là hình bình hành.
b) Ba đường thẳng $AC$, $BD$, $OM$ đồng quy.
a/ Ta có
\(AD\perp OA\) (AD là tiếp tuyến)
O là tâm đường tròn ngoại tiếp \(\Delta ABC\) => AO là trung tuyến của \(\Delta ABC\Rightarrow BC\perp AO\) (trong tg cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao)
=> AD//BC (cùng vuông góc với OA); mà AD=BC (gt) => ABCD là hình bình hành ( Tứ giác có 1 cặp cạnh đối // và bằng nhau thì tứ giác đó là hình bình hành)
b/ Do ABCD là hình bình hành nên AC cắt BD tại trung điểm mỗi đường
Mặt khác ta cũng có OM đi qua trung điểm của AC (Hai tiếp tuyến cùng xuất phát từ 1 điểm thì đường nối điểm đó với tâm đường tròn thì vuông góc và chia đôi dây cung nối 2 tiếp điểm)
=> AC; BD; OM đồng quy
) Có:
a)
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì MA=MC và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
Bài 1: Điểm C nằm giữa hai điểm A và B. Vẽ đường tròn tâm O, đường kính AB và đường tròn tâm O' đường kính BC. Vẽ tiếp tuyến chung của hai đường tròn tiếp xúc với đường tròn tâm O và tâm O' tại D và E. AD cắt BE tại M
a) tam giác MAB là tam giác j?
b) chứng minh CDME là hình chữ nhật và MC là tiếp tuyến của 2 đường tròn tâm O và tâm O'
c) Kẻ tia Ex vuông góc với EA và tia By vuông góc với BA. Ex cắt By tại N. Chứng minh 3 điểm D,C.N thẳng hàng.
Bài 2: Cho (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của (O) cắt (O') tại D. Tiếp tuyến tại A của (O') cắt (O) tại C. Chứng minh rằng:
a) tam giác ABC đồng dạng với tam giác DBA
b) (AC/AD)^2 ( AC trên AD tất cả mũ 2) = BC/BD( AC trên AD tất cả mũ 2 bằng BC/BD)
c) Gọi E là điểm đối xứng của A qua B. Chứng minh ACED là tứ giác nội tiếp.
Bài 1: CHo tứ giác ABCD có 2 đường chéo AC,BD vuông góc với nhau,Gọi M,N,P,Q là trung điểm của AB,BC,CD,DA.Chứng minh 4 điểm M,N,P,Q thuộc đường tròn
Bài 2: Cho tam giác ABC cân tại A.Nội tiếp đường tròn tâm O.Vẽ hình bình hành ABCD,tiếp tuyến tại C của đường tròn tâm O cắt đường thẳng AD tại N
a) Chứng minh AB là tiếp tuyến đường tròn tâm O
b) Chứng minh 3 đường thẳng AC,DB,ON cùng đi qua 1 điểm
Mọi người giúp em với ạ,em cảm ơn !
cho tam giác nhọn ABC đường tròn tâm o đường kính BC cắt AB,AC lần lượt tại D,E . hai đường thẳng BD và CE cắt nhau tại H . a,Chứng minh ADHE là tứ giác nội tiếp đường tròn
b,Chứng minh OD là tiếp tuyến của đường tròn ngoại tiếp tam giacs ADH
c,Cho góc BAC = 60 độ . chứng minh Sabc = Sade
Cho tam giác ABC có ba góc nhọn (AB<AC) nội tiếp đường tròn tâm O. Vẽ hai đường cao BN và CM cắt nhau tại H.
a) Chứng minh tứ giác AMHN và tứ giác BMNC nội tiếp đường tròn.
b) tiếp tuyến tại A cắt BC kéo dài tại I. Chứng minh IA2= IB.IC
c) Đường thẳng MN cắt đường tròn tâm O tại D và E ( điểm M nằm giữa hai điểm D và N). Chứng minh AD là tiếp tuyến của đường tròn ngoại tiếp tam giác DBM.