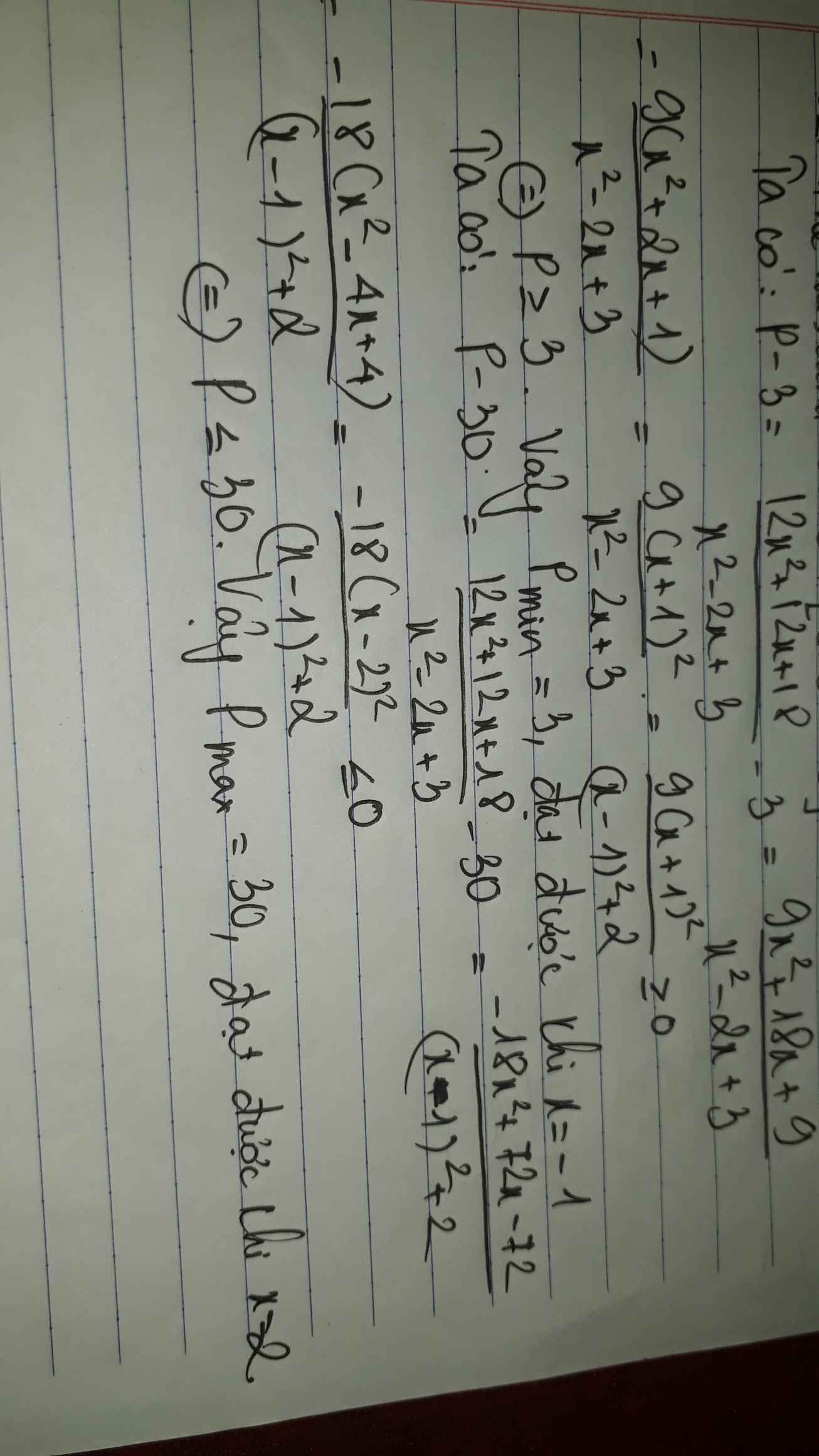tìm giá trị x biết 4|2x+3|=12x +28

Những câu hỏi liên quan
Tìm x, biết: (2x+4)(−12x)=0.
Giá trị của x cần tìm là ........... hoặc ..............
$(2x+4)(-12x)=0\\\Leftrightarrow \left[\begin{array}{1}2x+4=0\\-12x=0\end{array}\right.\\\Leftrightarrow\left[\begin{array}{1}2x=-4\\x=0\end{array}\right.\\\Leftrightarrow \left[\begin{array}{1}x=-2\\x=0\end{array}\right.\)
Vậy giá trị của \(x\) cần tìm là \(x=-2\) hoặc \(x=0\)
Đúng 0
Bình luận (0)
\(\left(2x+4\right)\left(-12x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\-12x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)
Đúng 2
Bình luận (0)
$(2x+4)(-12x)=0\\\Leftrightarrow \left[\begin{array}{1}2x+4=0\\-12x=0\end{array}\right.\\\Leftrightarrow\left[\begin{array}{1}2x=-4\\x=0\end{array}\right.\\\Leftrightarrow\left[\begin{array}{1}x=-2\\x=0\end{array}\right.$
Vậy giá trị của $x$ cần tìm là $x=-2$ hoặc $x=0$
Đúng 2
Bình luận (0)
Tìm x biết 4 |2x+3|=12x + 28
Tìm x biết
12x2+18x=-2x3Tìm giá trị nhỏ nhất của đa thức A=3x2+2x+4 phần 3Tìm số tự nhiên x biết:a, 128 – 3(x+4) 23b,
12
x
-
4
3
.
8
3
4
.
8
4
c, [(4x+28).3+55]:5 35d, 720:[41 – (2x – 5)] ...
Đọc tiếp
Tìm số tự nhiên x biết:
a, 128 – 3(x+4) = 23
b, 12 x - 4 3 . 8 3 = 4 . 8 4
c, [(4x+28).3+55]:5 = 35
d, 720:[41 – (2x – 5)] = 2 3 . 5
a, 128 – 3(x+4) = 23
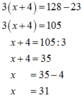
b, 12 x - 4 3 . 8 3 = 4 . 8 4
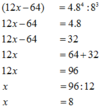
c, [(4x+28).3+55]:5 = 35
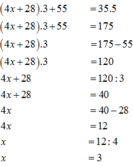
d, 720:[41 – (2x – 5)] = 2 3 . 5
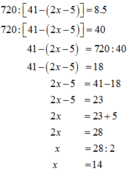
Đúng 0
Bình luận (0)
cho a=12x-2/4x+1
a)tính giá trị của A khi 2x-4=0
b)tìm giá trị của x để A=1
c)tìm x nguyên để Acó giá trị nguyên
a, A = \(\dfrac{12x-2}{4x+1}\)
2\(x\) - 4 = 0 ⇒ 2\(x\) = 4 ⇒ \(x\) = 4: 2 = 2
Giá trị của A tại 2\(x\) - 4 = 0 là giá trị của A tại \(x\) = 2
A = \(\dfrac{12\times2-2}{4\times2+1}\) = \(\dfrac{22}{9}\)
b, A = 1 \(\Leftrightarrow\) \(\dfrac{12x-2}{4x+1}\) = 1
12\(x\) - 2 = 4\(x\) + 1
12\(x\) - 4\(x\) = 1 + 2
8\(x\) = 3
\(x\) = \(\dfrac{3}{8}\)
c, A \(\in\) Z ⇔ 12\(x\) - 2 ⋮ 4\(x\) + 1
12\(x\) + 3 - 5 ⋮ 4\(x\) + 1
3.(4\(x\) + 1) - 5 ⋮ 4\(x\) + 1
5 ⋮ 4\(x\) + 1
Ư(5) ={-5; -1; 1; 5}
Lập bảng ta có:
| \(4x+1\) | -5 | -1 | 1 | 5 |
| \(x\) | -3/2 | -1/2 | 0 | 1 |
Vậy \(x\) \(\in\) {0; 1}
Đúng 2
Bình luận (0)
tìm tập hợp x thõa mãn A= ((12x-15)/(x2 -7x+12)) -((x+5)/(x-4)) + ((2x-3)/(3-x)) có giá trị nguyên
tìm x>0 thõa mãn /x-9/ + (-/2x/) = 0 ( dấu / / là gt tuyệt đối)
tìm x biết :
a, (x+1)2+2x(x-2)=3(x+4)(x+1)
chứng minh rằng biểu thức luôn dương với mọi giá trị của x
M=x2+12x+50
\(a,\left(x+1\right)^2+2x\left(x-2\right)=3\left(x+4\right)\left(x+1\right)\)
\(x^2+2x+1+2x^2-4x=3\left(x^2+5x+4\right)\)
\(3x^2-2x+1=3x^2+15x+12\)
\(\Rightarrow3x^2-2x+1-3x^2-15x-12=0\)
\(\Rightarrow-17x=11\)
\(\Rightarrow x=-\frac{11}{17}\)
\(b,M=x^2+12x+50\)
\(M=x^2+2.6.x+6^2+14\)
\(M=\left(x+6\right)^2+14\ge14>0\)
=> M luôn dương
Đúng 0
Bình luận (0)
\(\left(x+1\right)^2+2x\left(x-2\right)=3\left(x+4\right)\left(x+1\right).\)
\(\Leftrightarrow x^2+2x+1+2x^2-4x=3.(x^2+x+4x+4)\)
\(\Leftrightarrow x^2-2x+2x^2+1=3x^2+15x+12\)
\(\left(x^2-3x^2+2x^2\right)=\left(15x+2x\right)+12-1\)
\(17x+11=0\)
\(\Leftrightarrow x=\frac{-11}{17}\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức:
\(P=\dfrac{12x^2+12x+18}{x^2-2x+3}\)
tìm tất cả các giá trị của tham số a để phương trình x^4-4x^3-2x^2+12x+9-a=0 có 2 nghiệm pb