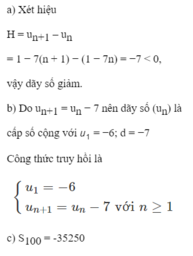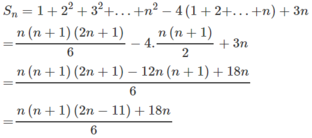công thức tính số số hạng và tổng của một dãy

Những câu hỏi liên quan
Các bn cho mình biết công thức để tính tổng một dãy số.
( Số các số hạng : .........; Tổng : ........... )
Trả lời
Số các số hạng
(số đầu-số cuối):khoảng cách+1=...
Tổng:
(số đầu+số cuối).số các số hạng:2=...
Học tốt !
Đúng 0
Bình luận (0)
. SỐ SỐ HẠNG = (Số cuối – Số đầu) : Đơn vị khoảng cách + 1
. TỔNG = (Số đầu + số cuối) x Số số hạng : 2
Đúng 0
Bình luận (0)
Cách tính ra tổng luôn khỏi cần bước số các số hạng thì làm như sau:
(số đầu+số cuối)x[(số đầu-số cuối):khoảng cách+1]:2
Học tốt nha !
Đúng 0
Bình luận (0)
Hãy nêu công thức :
a, Tính số số hạng của 1 dãy số cách đều
b, Tính tổng của dãy số cách đều
a.( số cuối - số đầu): khoảng cách+1
b.(số cuối + số đầu)x số số hạng :2
ai k mik mik k lại
good luck :)
Đúng 0
Bình luận (0)
a, (số cuối - số đầu) : khoảng cách + 1
b,(số cuối + số đầu)*số số hạng: 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Dãy số
u
n
cho bởi
u
1
3
,
u
n
+
1
1
+
u
n
2
,
n
1...
Đọc tiếp
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
a. Năm số hạng đầu của dãy số
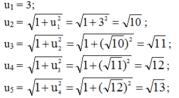
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
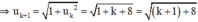
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
với
u
n
1
-
7
n
a) Khảo sát tính tăng, giảm của dãy số;b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;c) Tính tổng 100 số hạng đầu của dãy số.
Đọc tiếp
Cho dãy số ( u n ) với u n = 1 - 7 n
a) Khảo sát tính tăng, giảm của dãy số;
b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số;
c) Tính tổng 100 số hạng đầu của dãy số.
Tìm công thức tính số hạng tổng quát
u
n
theo n của dãy số sau
u
1
2
u
n
+
1
2...
Đọc tiếp
Tìm công thức tính số hạng tổng quát u n theo n của dãy số sau u 1 = 2 u n + 1 = 2 u n .
A. u n = n 2 − 3 n + 10
B. u n = 2 n
C. u n = 2 n
D. u n = n + 2
* Ta có:
u 2 = 2 u 1 = 2.2 = 4 = 2 2 u 3 = 2 u 2 = 2.4 = 8 = 2 3 u 4 = 2 u 3 = 2.8 = 16 = 2 4 u 5 = 2 u 4 = 2.16 = 32 = 2 5
Từ các số hạng đầu tiên, ta dự đoán số hạng tổng quát u n có dạng: u n = 2 n ∀ n ≥ 1 ∗
* Ta dùng phương pháp chứng minh quy nạp để chứng minh cộng thức (*) đúng.
Với n=1 ; có: u 1 = 2 1 = 2 (đúng). Vậy (*) đúng với n= 1
Giả sử (*) đúng với n= k , có nghĩa ta có: u k = 2 k (2)
Ta cần chứng minh (*) đúng với n = k+1. Có nghĩa là ta phải chứng minh: u k + 1 = 2 k + 1 .
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = 2 u k = 2 . 2 k = 2 k + 1
Vậy (*) đúng với n = k+1. Kết luận (*) đúng với mọi số nguyên dương n.
Chọn đáp án B.
Đúng 0
Bình luận (0)
tìm các công thúc của dãy số :
1. công thức tìm số số hạng
2. công thức tìm tổng
3. công thức tìm 1 số hạng bất kì
4.công thức tìm số đó đứng thứ mấy
1; Số số hạng = (số cuối - số đầu) : khoảng cách + 1
2; tổng = (số cuối + số đầu)\(\times\) số số hạng : 2
3; số thứ n = khoảng cách \(\times\)(n-1) + số đầu
4 tìm số đó đứng thứ mấy
vị trí của số cần tìm: (số đó - số đầu): khoảng cách + 1
Đúng 3
Bình luận (0)
1.SSH = ( SC - SĐ ) : KC + 1
2.T = ( SĐ + SC ) x SSH :2
3.STn = ( n - 1 ) x KC + SĐ
4. Số đó đứng thứ mấy = ( Số đó - SĐ ) : KC +1
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho dãy số
(
u
n
)
với
u
n
n
2
-
4
n
+
3
a) Viết công thức truy hồi của dãy số;b) Chứng minh dãy số bị chặn dưới;c) Tính tổng n số hạng đầu của dãy đã cho.
Đọc tiếp
Cho dãy số ( u n ) với u n = n 2 - 4 n + 3
a) Viết công thức truy hồi của dãy số;
b) Chứng minh dãy số bị chặn dưới;
c) Tính tổng n số hạng đầu của dãy đã cho.
Tìm công thức tính số hạng tổng quát
u
n
theo n của dãy số sau
u
1
3
u
n
+
1
u...
Đọc tiếp
Tìm công thức tính số hạng tổng quát u n theo n của dãy số sau u 1 = 3 u n + 1 = u n + 2
A. u n = 3 n + n 2 - 1
B. u n = 2 n + 1
C. u n = 4 n - 10
D. Đáp án khác
Ta có:
u 2 = u 1 + 2 = 3 + 2 = 5.
u 3 = u 2 + 2 = 5 + 2 = 7.
u 4 = u 3 + 2 = 7 + 2 = 9.
u 5 = u 4 + 2 = 9 + 2 = 11.
Từ các số hạng đầu trên, ta dự đoán số hạng tổng quát u n có dạng:
u n = 2 n + 1 ∀ n ≥ 1 ∗
Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.
Với n =1 ; u 1 = 2 . 1 + 1 = 3 (đúng). Vậy (*) đúng với n =1
Giả sử (*) đúng với n =k. Có nghĩa ta có: u k = 2 k + 1 (2)
Ta cần chứng minh (*) đúng với n = k+1 - có nghĩa là ta phải chứng minh:
u k + 1 = 2(k+1)+1= 2k + 3
Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:
u k + 1 = u k +2 = 2k +1 +2 = 2k + 3
Vậy (*) đúng khi n = k+1 .
Kết luận (*) đúng với mọi số nguyên dương n.
Đáp án B
Đúng 0
Bình luận (0)
Bài toán yêu cầu bạn tính tổng của một cấp số nhân có công bội là 3 và số hạng đầu tiên là 3. Công thức tính tổng của một cấp số nhân là:
$$S_n frac{a_1(1-q^n)}{1-q}$$
Trong đó, $a_1$ là số hạng đầu tiên, $q$ là công bội, và $n$ là số hạng. Áp dụng công thức này vào bài toán của bạn, ta có:
$$A 3^1 + 3^2 + 3^3 + ....... + 3^50 frac{3(1-3^{50})}{1-3}$$
Để tính giá trị của A, bạn có thể sử dụng máy tính hoặc các trang web chuyên về toán học. Mình đã tìm thấy một trang web có thể giải quyết...
Đọc tiếp
Bài toán yêu cầu bạn tính tổng của một cấp số nhân có công bội là 3 và số hạng đầu tiên là 3. Công thức tính tổng của một cấp số nhân là:
$$S_n = \frac{a_1(1-q^n)}{1-q}$$
Trong đó, $a_1$ là số hạng đầu tiên, $q$ là công bội, và $n$ là số hạng. Áp dụng công thức này vào bài toán của bạn, ta có:
$$A = 3^1 + 3^2 + 3^3 + ....... + 3^50 = \frac{3(1-3^{50})}{1-3}$$
Để tính giá trị của A, bạn có thể sử dụng máy tính hoặc các trang web chuyên về toán học. Mình đã tìm thấy một trang web có thể giải quyết bài toán này cho bạn. Theo trang web đó, kết quả của A là:
$$A \approx 7.178979876e23$$
Đây là một số rất lớn, gần bằng 718 nghìn tỷ tỷ tỷ. Hy vọng bạn đã hiểu cách giải bài toán này. Nếu bạn có thắc mắc gì khác, xin vui lòng liên hệ với mình. Mình rất vui khi được giúp đỡ bạn